The Do While loop is used any time we want to make sure that the instructions will be executed at least once, even if the condition of the loop evaluates as False. As we learned in the previous lesson, a loop is a construct that lets us run one or more instructions repeatedly, until a condition is evaluated as False.
The general form of a Do While loop looks like this:
|
1 2 3 4 |
do { instructions; } while (condition); |
If you compare this to the While loop explained in the previous post, you will easily notice that the conditional check is performed AFTER the execution of the instructions in the loop body. This means that the instructions will be executed AT LEAST ONCE, even if the condition will evaluate as False.
First, the program will run the instructions, that it will evaluate the condition. If the condition returns True, it will run the instructions again; if not, the code execution will jump to the first instruction that follows after the Do While loop.
Lets show an example of usage for Do While loops, calculating the factorials of a number:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
Console.Write("n = "); //print a message int n = int.Parse(Console.ReadLine()); //read the number input by user decimal factorial = 1; do { factorial *= n; n--; } while (n > 0); //calculate the factorial Console.WriteLine("n! = " + factorial); //display the result Console.Read(); |
If you remember from mathematics, the factorial of an integer positive number is the product of all the integers greater than 0 and less than or equal to the number itself. For instance, the factorial of 3 is:
|
1 |
3! = 1 * 2 * 3; |
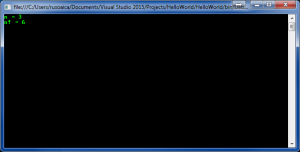
So, the above code will display the following output:
When the program runs, it first starts with a result of 1, then a consequent multiplication of the result of each iteration of the loop, while reducing n by 1, until it reaches 0. This gives us the product n * (n-1) * … * 1.
This piece of code always runs at least once, that’s why it will not work properly when n is less than or equal to 0.
The concepts explained in this lesson are also shown visually as part of the following video:
EXERCISES
1. Write a program that calculates with how many zeroes the factorial of a given number ends. Examples:
N = 10 -> N! = 3628800 -> 2
N = 20 -> N! = 2432902008176640000 -> 4.
Solution
Guidelines: The number of zeros at the end of n! depends on how many times the number 10 is a divisor of the factorial. Because the product 1*2*3…*n has a greater number of divisors 2, than 5 and because 10 = 2 * 5, then the number of zeros in n! is exactly as many as the multipliers with value 5 in the product 1 * 2 * 3 * … * n. Because every fifth number is divisible by 5, and every 25th number is divisible by 5 two times, etc., the number of zeros in n! is the sum: n/5 + n/25 + n/125 + …
2. Write a program that asks user for an integer input representing the number of a month (1-12), until the input integer is correct, then display it.
Solution
Guidelines: Use a do…while loop, in which you check if the input value is in the accepted range. If not, prompt for input again.
Tags: do while loop, loops
