Recursivitatea este un concept matematic care definește orice obiect care este conținut sau definit de el însuși. Aceasta ar trebui să fie definiția oficială, academică. În cuvinte simple, funcțiile recursive sunt funcții care fac apel la ele însele din interiorul corpului lor, pentru a rezolva o problemă.
Funcțiile recursive, atunci când sunt create în mod corect, ne pot ajuta să rezolvăm probleme foarte complicate, care ar necesita un volum mult mai mare de cod dacă le-am rezolva în alt mod, si ne pot ajuta să scriem un cod elegant, ușor de înțeles. Să luăm un exemplu de recursivitate. Câți dintre voi încă vă mai amintesc numerele lui Fibonacci? Așa ma gândeam și eu 😀
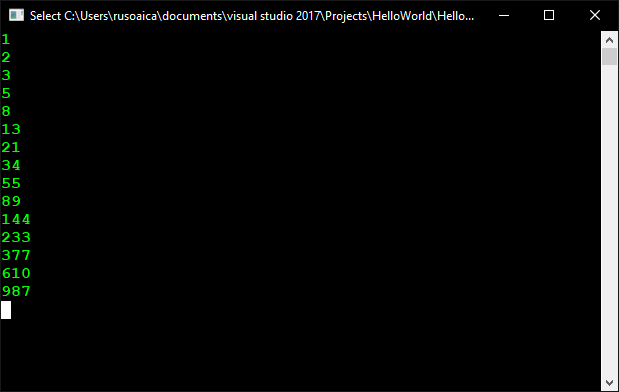
Numerele lui Fibonacci sunt o secvență de numere în care fiecare element nou este suma celor două elemente anterioare. De exemplu: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, etc. Imaginați-vă acum că va trebui să calculați secvența Fibonacci până la 1000. Veți sfârși în cele din urma cu ceva de genul:
class Program
{
static void Main(string[] args)
{
int numar = 16; //numarul elementelor Fibonacci
int[] Fib = new int[numar + 1];
//initializeaza primele doua elemente
Fib[0] = 0;
Fib[1] = 1;
for (int i = 2; i <= numar; i++)
{
Fib[i] = Fib[i - 2] + Fib[i - 1];
Console.WriteLine(Fib[i - 2] + Fib[i - 1]);
}
Console.Read();
}
}
Iar rezultatul ar fi acesta:
Singura problemă cu codul de mai sus este că trebuie să știm în prealabil câte elemente dorim să calculăm în secvență. Pentru numărul 1000, există 15 astfel de elemente. Dar dacă am fi vrut să-l calculăm pentru un număr mult mai mare, cum ar fi 1.000.000? Am avea nevoie de o mulțime de teste pentru a vedea câte elemente se încadrează în acel interval. Și acest lucru nu este elegant dacă dorim o soluție dinamică, pentru orice număr.
Deci .. Vă prezint … pam-pam-paaaam! Funcții recursive! Iată un exemplu de bază:
static void Main(string[] args)
{
CalculeazaFibonacci(10);
Console.Read();
}
static long CalculeazaFibonacci(int n)
{
if (n <= 2)
return 1;
return CalculeazaFibonacci(n - 1) + CalculeazaFibonacci(n - 2);
}
Vedeți cât de scurtă este funcția noastră? Doar 3 linii de cod. Acesta este un exemplu perfect pentru modul în care recursivitatea ne poate ajuta, dar și un exemplu clasic de implementare greșită și extrem de ineficientă a recursivității. Acest lucru se datorează faptului că există multe calcule excesive ale unuia și aceluiași element al secvenței. Vom aborda aceste avantaje și dezavantaje ale recursivității mai târziu.
Există două tipuri de recursivitate:
- recursivitate directă – atunci când avem un apel la aceeași funcție din corpul acelei funcții
- recursivitate indirectă – atunci când avem funcția A, care apelează funcția B, care apelează funcția C, care în schimb apelează din nou funcția A, creând un fel de inel. Aceste funcții sunt numite și reciproc recursive .
Ca și în cazul buclelor infinite, funcțiile recursive dețin, de asemenea, pericolul de recursivitate infinită. Ori de câte ori folosiți recursivitatea, trebuie să vă asigurați că specificați cel puțin un caz atunci când obțineți un rezultat concret, care nu are nevoie de un alt apel recursiv. Cu alte cuvinte, cel puțin un caz în care recursivitatea este terminată. Programatorii numesc acest caz specific fundul recursivității. În exemplul nostru anterior, fundul recursiunii este atunci când variabila n atinge o valoare mai mică sau egală cu 2. Dacă nu specificați un fund al al recursiunii, probabil că veți sfârși cu o excepție StackOverflowException.
Deci, cum creăm o funcție recursivă? Ca și în cazul oricărei alte sarcini de programare, trebuie să împărțiți sarcina pe care încercați să o rezolvați în sub-sarcini, pentru soluția cărora putem folosi același algoritm, ca într-un tipar. În final, combinația tuturor subsarcinilor ar trebui să conducă la rezolvarea sarcinii inițiale. Pentru fiecare sub-sarcină, calculul trebuie modificat astfel încât la un moment dat să fie atins fundul recursiunii.
Acum, că am stabilit că avem nevoie de un tipar oarecare pentru a putea crea o recursivitate, să încercăm un alt exemplu. Și, îmi pare rău, matematică din nou… De data aceasta, vom calcula numere factoriale. Ce sunt ele? Un număr factorial n (scris n!) este produsul tuturor numerelor întregi între 1 și n inclusiv. Există o singură excepție, 0! este prin definiție 1. Ca și concept de bază, putem scrie acest lucru ca fiind:
n! = 1 * 2 * 3 * ... * n
Aceasta este definiția generală, dar cum putem identifica un tipar pe care îl putem folosi pentru implementarea noastră recursivă? Să luăm reprezentarea discretă a câtorva elemente:
0! = 1 1! = 1 = 1 * 1 = 1 * 0! 2! = 2 * 1 = 2 * 1! 3! = 3 * 2 * 1 = 3 * 2! 4! = 4 * 3 * 2 * 1 = 4 * 3! 5! = 5 * 4 * 3 * 2 * 1 = 5 * 4! 6! = 6 * 5 * 4 * 3 * 2 * 1 = 6 * 5!
si asa mai departe. Și acum, putem vedea clar că există următorul model:
n! = n * (n - 1)!
Din aceasta putem spune că fundul recursivității va fi ultimul caz al secvenței, n = 0, atunci când valoarea factorialului este egală cu 1. Suntem siguri că recursiunea noastră nu va fi infinită, deoarece, pentru fiecare recursiune, calculăm n – 1 și multiplicăm rezultatul cu n, iar scăderea succesivă a lui 1 din n va duce în cele din urmă la 0, fundul recursiunii noastre. În acest moment, putem scrie următoarea funcție:
static void Main(string[] args)
{
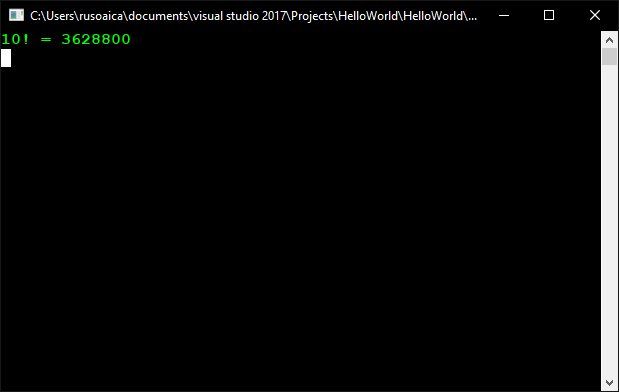
decimal factorial = Factorial(10);
Console.WriteLine("{0}! = {1}", 10, factorial);
Console.Read();
}
static decimal Factorial(int n)
{
if (n == 0) // fundul recursiunii
return 1;
else // apel recursiv: functia se apeleaza pe ea insasi
return n * Factorial(n - 1);
}
și acesta este rezultatul:
Cu toate acestea, ca și în exemplul nostru Fibonacci, aceasta este, de asemenea, o implementare proastă a recursivității, chiar dacă la explicarea funcțiilor recursive, numerele factoriale sunt exercițiile preferate în universități. De aceea vă voi explica alternativa, utilizând iterații, care în acest caz sunt mai eficiente. Singura diferență este că iterația nu este la fel de intuitivă ca recursiunea.
static decimal Factorial(int n)
{
decimal rezultat = 1;
for (int i = 1; i <= n; i++)
rezultat = rezultat * i;
return result;
}
Ceea ce trebuie să vă amintiți este că, deși recursiunea este un instrument puternic, iterația, atunci când este posibilă, este mai eficientă. De aceea, ori de câte ori puteți adapta o bucată de cod pentru a utiliza iterația în locul recursivității, faceți-o. Programul dvs. va rula mai repede.
Să ne uităm la un alt exemplu în care am putea folosi recursivitatea pentru a rezolva problema. De data aceasta vom lua în considerare și o soluție iterativă. Dacă vă aduceți aminte de lecția bucle imbricate, am avut acolo ceva de genul:
for (a1 = 1; a1 <= K; a1++)
for (a2 = 1; a2 <= K; a2++)
for (a3 = 1; a3 <= K; a3++)
…
for (aN = 1; aN <= K; aN++)
Console.WriteLine("{0} {1} {2} … {N}", a1, a2, a3, …, aN);
Exemplul de mai sus este ușor de înțeles, avem bucle imbricate care sunt ușor de implementat atunci când știm deja numărul de bucle de care avem nevoie. Dar când nu știm acest lucru, încep să apară probleme. Dacă vrem să căutăm un fișier pe hard disk, pornind de la un director rădăcină, am putea folosi buclele pentru fiecare nivel nou din arborele de directoare, dar numai dacă știm în prealabil cât de adânc este ramificat și cât de adânc buclele trebuie să meargă. Dar nu știm, ceea ce face implementarea dificilă sau imposibilă.
Deci, încercând să rezolvăm problema, putem spune că avem nevoie de un set de instrucțiuni pentru un număr de N bucle imbricate, de la 1 la K. Ca exemplu, atunci când N = 2 și K = 3 (adică „două bucle imbricate, de la 1 până la K”) și, de asemenea, atunci când N = 3 și K = 3, acesta ar trebui să fie rezultatul:
1 1 1 1 1
1 2 1 1 2
1 3 1 1 3
N = 2 2 1 N = 3 1 2 1
K = 3 -> 2 2 K = 3 -> …
2 3 3 2 3
3 1 3 3 1
3 2 3 3 2
3 3 3 3 3
Fiecare rând al rezultatului poate fi considerat secvență ordonată a numerelor N. Primul reprezintă valoarea curentă a contorului buclei, al doilea – al celei de-a doua bucle, etc. La fiecare poziție, putem avea valori între 1 și K. Soluția sarcinii noastre se reduce la găsirea tuturor secvențelor ordonate ale N elemente pentru N și K date. Când căutăm o soluție recursivă la această problemă, prima problemă cu care ne confruntăm este găsirea unei dependențe recurente. Să examinăm mai atent exemplul din această sarcină și să-i acordăm o atenție suplimentară. Observați că dacă am calculat răspunsul pentru N = 2, atunci răspunsul pentru N = 3 poate fi obținut dacă punem pe prima poziție fiecare dintre valorile K (în acest caz de la 1 la 3), iar pe celelalte două poziții punem fiecare dintre cuplurile de numere produse pentru N = 2. Putem verifica dacă această regulă se aplică pentru numere mai mari de 3. Astfel am obținut următoarea dependență – începând de la prima poziție, punem pe poziția fiecăreia dintre valorile de la 1 la K și continuarea recursiv cu următoarea poziție. Aceasta continuă până când ajungem în poziția N, după care vom imprima rezultatul obținut (fundul recursiunii). Iată cum arată metoda implementată în C#:
static void BubleImbricate(int iteratiaCurenta)
{
if (iteratiaCurenta == numarBucle)
{
AfiseazaBucle();
return;
}
for (int contor = 1; contor <= numarIteratii; contor++)
{
bucle[iteratiaCurenta] = contor;
BubleImbricate(iteratiaCurenta + 1);
}
}
Vom păstra secvența de valori într-un array numit bucle, care vor fi imprimate pe consolă prin metoda AfiseazaBucle() atunci când este necesar. Metoda BubleImbricate() ia un parametru ce indică poziția în care vom plasa valorile. În buclă plasăm consecutiv pe poziția curentă fiecare dintre valorile posibile (variabila numarIteratii conține valoarea lui K, introdusă de utilizator), după care apelăm recursiv metoda BubleImbricate() pentru următoarea poziție. Fundul recursiunii este atins atunci când poziția curentă devine N (variabila numarIteratii conține valoarea lui N introdusă de utilizator). În acest moment avem valori pe toate pozițiile și tipărim secvența. Iată o implementare completă a soluției recursive cu bucle imbricate:
static int numarBucle;
static int numberOfIterations;
static int[] bucle;
static void Main(string[] args)
{
Console.Write("N = ");
numarBucle = int.Parse(Console.ReadLine());
Console.Write("K = ");
numarIteratii = int.Parse(Console.ReadLine());
bucle = new int[numarBucle];
BubleImbricate(0);
Console.Read();
}
static void BubleImbricate(int iteratiaCurenta)
{
if (iteratiaCurenta == numarBucle)
{
AfiseazaBucle();
return;
}
for (int contor = 1; contor <= numarIteratii; contor++)
{
bucle[iteratiaCurenta] = contor;
BubleImbricate(iteratiaCurenta + 1);
}
}
static void AfiseazaBucle()
{
for (int i = 0; i < numarBucle; i++)
Console.Write("{0} ", bucle[i]);
Console.WriteLine();
}
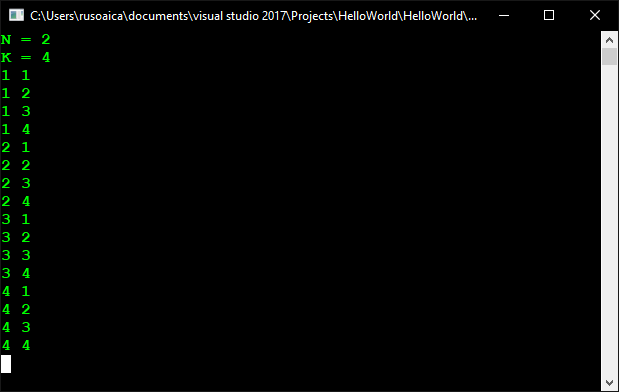
Dacă rulați aplicația și introduceți N și K respectiv 2 și 4, vom obține următorul rezultat:
În metoda Main() introducem valori pentru N și K, creăm o matrice în care vom păstra succesiunea valorilor, după care apelăm metoda BubleImbricate(), pornind de la prima poziție. Observați că setăm 0 ca parametru al array-ului, deoarece păstrăm secvența de valori într-un array și după cum deja știm, numărarea elementelor de array începe de la 0. Metoda AfiseazaBucle() iterează toate elementele array-ului și le imprimă pe consolă.
Acum, că am văzut cum arată buclele imbricate folosind recurivitatea, să aruncăm o privire asupra celui de-al doilea mod de a implementa buclele imbricate, iterația. Pentru implementarea unei soluții iterative a buclelor imbricate, putem folosi următorul algoritm care găsește următoarea secvență de numere și o imprimă la fiecare iterație:
- La începutul fiecărei poziții plasează numărul 1.
- Imprimă secvența curentă de numere.
- Incrementează cu 1 numărul din poziția N. Dacă valoarea obținută este mai mare decât K, înlocuiește cu 1 și incrementează cu 1 valoarea din poziția N – 1. Dacă valoarea sa a devenit mai mare decât K, înlocuiește cu 1 și incrementează cu 1 valoarea în poziția N – 2, etc.
- Dacă valoarea primei poziții a devenit mai mare decât K, algoritmul își încheie lucrarea.
- Revine la pasul 2.
Mai jos propun o implementare simplă a algoritmului iterativ al buclei imbricate descrise:
static int numarBucle;
static int numarIteratii;
static int[] bucle;
static void Main(string[] args)
{
Console.Write("N = ");
numarBucle = int.Parse(Console.ReadLine());
Console.Write("K = ");
numarIteratii = int.Parse(Console.ReadLine());
bucle = new int[numarBucle];
BucleImbricate();
Console.Read();
}
static void BucleImbricate()
{
InitiazaBucle();
int pozitieCurenta;
while (true)
{
AfiseazaBucle();
pozitieCurenta = numarBucle - 1;
bucle[pozitieCurenta] = bucle[pozitieCurenta] + 1;
while (bucle[pozitieCurenta] > numarIteratii)
{
bucle[pozitieCurenta] = 1;
pozitieCurenta--;
if (pozitieCurenta < 0)
return;
bucle[pozitieCurenta] = bucle[pozitieCurenta] + 1;
}
}
}
static void InitiazaBucle()
{
for (int i = 0; i < numarBucle; i++)
bucle[i] = 1;
}
static void AfiseazaBucle()
{
for (int i = 0; i < numarBucle; i++)
Console.Write("{0} ", bucle[i]);
Console.WriteLine();
}
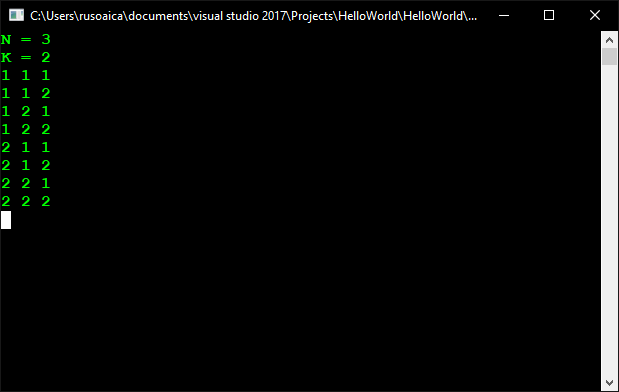
Metodele Main() și AfiseazaBucle() sunt aceleași ca și în implementarea soluției recursive. Metoda BucleImbricate() este diferită. Implementează acum algoritmul pentru rezolvarea iterativă a problemei, și din acest motiv nu primește parametri, spre deosebire de versiunea recursivă. La începutul acestei metode numim metoda InitiazaBucle(), care iterează elementele array-ului și pune în fiecare poziție 1. Efectuăm pașii algoritmului într-o buclă infinită, din care vom scăpa la momentul potrivit, încheind executărea metodelor prin folosirea operatorului return. Modul în care implementăm pasul 3 al algoritmului este foarte interesant. Implementăm verificarea valorilor mai mari decât K, înlocuirea lor cu 1 și incrementarea cu 1 a valorii pe poziția anterioară (după care facem aceeași verificare și pentru ea) utilizând o buclă While, în care intrăm numai dacă valoarea este mai mare decât K. Pentru acest scop, vom înlocui mai întâi valoarea poziției curente cu 1. După aceea, poziția de dinainte devine poziția curentă. Apoi vom incrementa valoarea pe noua poziție cu 1 și vom reveni la începutul buclei. Aceste acțiuni continuă până când valoarea de pe poziția curentă nu este mai mică sau egală cu K (numărul numarIteratii conține valoarea lui K), moment când vom ieși din buclă. Atunci când valoarea primei poziții devine mai mare decât K (acesta este momentul în care trebuie să terminăm execuția), în locul ei punem 1 și încercăm să incrementăm valoarea pe poziția anterioară. În acest moment valoarea variabilei pozitieCurenta devine negativă (deoarece prima poziție a array-ului este 0) și terminăm execuția metodei folosind operatorul return. Acesta este sfârșitul sarcinii noastre. Acum o putem testa cu N = 3 și K = 2, de exemplu:
Deci, în cele din urmă, care este mai bună? Iterația sau recursivitatea?
Dacă algoritmul de rezolvare a problemei este recursiv, implementarea soluției recursive poate fi mult mai lizibilă și mai elegantă decât soluția iterativă a aceleași probleme. Uneori definirea unui algoritm echivalent este mult mai dificilă și nu este ușor să se demonstreze că cei doi algoritmi sunt echivalenți. În anumite cazuri, folosind recursivitatea, putem realiza soluții mult mai simple, mai scurte și ușor de înțeles. Pe de altă parte, apelurile recursive pot consuma mult mai multe resurse (timp CPU și memorie). În anumite situații, soluțiile recursive pot fi mult mai greu de înțeles și de urmat decât soluțiile iterative relevante. Recursivitatea este o tehnică de programare puternică, dar trebuie să ne gândim cu atenție înainte de a o folosi. Dacă este folosită în mod incorect, poate duce la soluții ineficiente și greu de înțeles și de întreținut.
Am spus la începutul acestei lungi lecții că voi explica mai pe îndelete de ce exemplul numărului lui Fibonacci este ineficient. Dacă am seta în exemplul nostru valoarea n = 100, calculele ar lua atât de mult timp încât nimeni nu ar aștepta să vadă rezultatul. Motivul este că o implementare similară este extrem de ineficientă. Fiecare apel recursiv duce la alte două apeluri și fiecare dintre aceste apeluri determină încă două apeluri și așa mai departe. De aceea arborele de apeluri crește exponențial, după cum se arată în figura de mai jos. Numărul de pași pentru calculul fib(100) este de ordinul 1,6 ridicat la puterea 100 (acest lucru ar putea fi dovedit matematic), în timp ce, dacă soluția este liniară, numărul de pași ar fi doar 100. Problema vine din faptul că există o mulțime de calcule excesive. Puteți observa că fib(2) apare de mai multe ori pe arborele Fibonacci:
Acum, să vorbim puțin despre implementarea corectă a unei astfel de soluții recursive. Putem optimiza metoda recursivă pentru calcularea numerelor Fibonacci prin memorarea (salvarea) numerelor deja calculate într-un array, și efectuarea unui apel recursiv numai dacă numărul pe care încercăm să-l calculăm nu a fost deja calculat. Datorită acestei mici tehnici de optimizare (cunoscută în domeniul informaticii și optimizării dinamice ca memoization (a nu se confunda cu memorization) soluția recursivă ar funcționa pentru numărătoarea liniară a pașilor. Iată o astfel de implementare:
static long[] numere;
static void Main(string[] args)
{
Console.Write("n = ");
int n = int.Parse(Console.ReadLine());
numere = new long[n + 2];
numere[1] = 1;
numere[2] = 1;
long resultat = Fib(n);
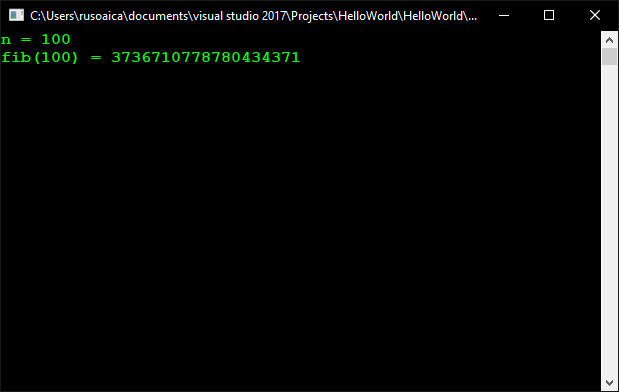
Console.WriteLine("fib({0}) = {1}", n, resultat);
Console.Read();
}
static long Fib(int n)
{
if (0 == numere[n])
numere[n] = Fib(n - 1) + Fib(n - 2);
return numere[n];
}
Observați diferența? În timp ce în versiunea inițială, dacă n = 100, se părea că execuția continuă pentru eternitate, soluția optimizată obține un răspuns instantaneu. După cum vom învăța mai târziu, prima soluție rulează în timp exponențial, în timp ce a doua este liniară:
Putem chiar să îmbunătățim conceptul precedent de păstrare a valorilor anterioare ale numerelor. Nu este greu de observat că putem rezolva problema fără a folosi recursivitatea, calculând consecutiv numerele Fibonacci. În acest scop, vom păstra numai ultimele două elemente calculate ale secvenței și le vom folosi pentru a obține următorul element. Mai jos puteți vedea o implementare a algoritmului iterativ de calcul al numerelor Fibonacci:
static void Main(string[] args)
{
Console.Write("n = ");
int n = int.Parse(Console.ReadLine());
long result = Fib(n);
Console.WriteLine("fib({0}) = {1}", n, result);
Console.Read();
}
static long Fib(int n)
{
long fn = 0;
long fnMinus1 = 1;
long fnMinus2 = 1;
for (int i = 2; i < n; i++)
{
fn = fnMinus1 + fnMinus2;
fnMinus2 = fnMinus1;
fnMinus1 = fn;
}
return fn;
}
Această soluție nu este doar scurtă și elegantă, ci ascunde și riscurile recursivității. În plus, este eficientă și nu necesită memorie suplimentară. Ca și concluzie a exemplelor anterioare, vă pot oferi următoarea recomandare:
Evitați recursivitatea, cu excepția cazului în care sunteți siguri de modul în care funcționează și de ceea ce trebuie să se întâmple în fundal. Recursivitatea este o armă puternică, cu care puteți cu ușurință să vă împușcați propriul picior (au!). Utilizați-o cu atenție!
Pentru a încheia această lecție, să vedem un exemplu pe care l-am sugerat deja, căutarea unui fișier într-un director cu subdirectoare:
using System;
using System.IO;
namespace HelloWorld
{
class Program
{
static void Main(string[] args)
{
Console.Read();
cautaDirector(@"C:\", "test.txt");
}
static void cautaDirector(string directorRadacina, string numeFisier)
{
try
{
foreach (string director in Directory.GetDirectories(directorRadacina))
{
foreach (string fisier in Directory.GetFiles(director, numeFisier))
{
Console.WriteLine(fisier);
}
cautaDirector(director, numeFisier);
}
}
catch (System.Exception excpt)
{
Console.WriteLine(excpt.Message);
}
}
}
}
În codul de mai sus, există câteva lucruri noi despre care încă nu am vorbit, cum ar fi instrucțiunea try…catch, și ar trebui să o ignorați. O veți înțelege mai bine când va veni timpul. De asemenea, trebuie să observați că am folosit instrucțiunea using System.IO;, deoarece folosim funcții cum ar fi Directory.GetDirectories(), care se află în ansamblul System.IO. Nu vă faceți griji nici despre ea, deocamdată. Tot ce mi-a rămas de specificat este că deși nu am învățat încă despre ele, instrucțiunile Directory.GetDirectories() și Directory.GetFiles() fac exact asta: returnează o listă de directoare, respectiv fișiere, dintr-o anumită cale pe care o specificăm. Așa cum am învățat în lecția iterarea elementelor unui array, folosim o buclă Foreach pentru a trece prin toate elementele din lista returnată de instrucțiunea Directory.GetDirectories(). Apoi, pentru fiecare dintre aceste directoare, folosim o altă buclă Foreach, pentru a itera prin lista tuturor fișierelor care corespund criteriilor de căutare, conținute în acel director, listă furnizată de Directory.GetFiles(). Acesta este locul în care imprimăm fișierele găsite la consolă. Totuși, ceea ce face ca această metodă să fie recursivă este faptul că la fiecare iterație a buclei Foreach care trece prin directoare, apelăm din nou metoda cautaDirector, cu directorul curent al iteratației. Aceasta înseamnă că bucla curentă va aștepta până la terminarea acestui nou apel la metodă și numai după aceea își va relua ciclarea. Desigur, dacă în noul apel, metoda Directory.GetFiles() va conține o nouă listă de directoare (subdirectoarele din directorul pe care l-am folosit în prima buclă, atunci când am apelat metoda), bucla foreach va apela funcția din nou, pentru fiecare dintre aceste directoare, și așa mai departe. Aceasta înseamnă că, dacă avem un arbore de directoare, funcția va trece recursiv prin toate acestea.
Tags: funcții, funcții recursive

Cum fac funcția de mai jos doar recursiv, într-o singură funcție?
int numar(int n,int c1,int c2)
{
int v[9],c=-1,i;
while (n)
{
v[++c]=n%10;
n/=10;
}
for (i=0;i=0;–i)
n=n*10+v[i];
return n;
}
Bună și ție!
Funcția de mai nu face sens. În primul rând, folosește C, nu C#, care este predat pe acest site. În al doilea rând, la bucla for, i = 0 la condiția de încheiere n-are nici un sens. Și în al treilea rând, acțiunea de la sfârșit, -i, la fel, nu are sens.
Două puncte: dacă adaugi niște comentarii prin cod, poate lumea chiar reușește să înțeleagă ce vrea să facă respectivul cod, fără să stea o oră să descifreze și să ghicească; să spui „bună!” și „te rog”/„mulțumesc” pot aduce mai multă cooperare, chiar și atunci când cererea pare destul de evident mai degrabă din categoria „mi-am găsit mașină de scris teme” decât „nu am înțeles, am nevoie de lămuriri”.