Recursion is a mathematical concept that defines any object that is contained or defined by itself. That should be the official, academic definition. In simple words, recursive functions are functions that make a call to themselves from within their own body, in order to solve a problem.
Recursive functions, when done correctly, can help us solve really complicated problems and can help us write elegant code and solve problems that would require a lot of code if done otherwise. Lets take an example of recursiveness. How many of you still remember the Fibonacci’s numbers? I thought so too 😀
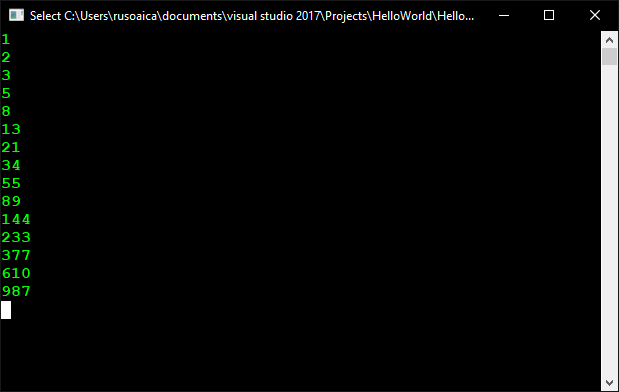
Fibonacci’s numbers are a sequence of numbers in which each new element is the sum of its previous two elements. For instance: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, etc. Imagine now you would have to calculate the Fibonacci sequence up until 1000. Not that hard, you will probably end up with something like this:
class Program
{
static void Main(string[] args)
{
int number = 16; //the number of Fibonacci elements
int[] Fib = new int[number + 1];
//assign the first two elements
Fib[0] = 0;
Fib[1] = 1;
for (int i = 2; i <= number; i++)
{
Fib[i] = Fib[i - 2] + Fib[i - 1];
Console.WriteLine(Fib[i - 2] + Fib[i - 1]);
}
Console.Read();
}
}
And the output would be this one:
The only problem with the above code is that we need to know how many elements do we want to calculate in the sequence. For the number 1000, there are 15 of such elements. But what if we wanted to calculate it for a much larger number, like 1,000,000? We would need a lot of tests to see how many elements fit in that range. And this is not elegant if we want a dynamic solution, for any number.
So.. Introducing you… pam-pam-paaaam! Recursive functions! Here is a basic example:
static void Main(string[] args)
{
CalculateFibonacci(10);
Console.Read();
}
static long CalculateFibonacci(int n)
{
if (n <= 2)
return 1;
return CalculateFibonacci(n - 1) + CalculateFibonacci(n - 2);
}
See how short is our function? Only 3 lines of code. This is a perfect example of how recursion can help us, but also a classic example of a very bad and highly inefficient implementation of recursion. This is because there are many excessive calculations of one and the same element of the sequence. We will address these advantages and disadvantages of recursion later on.
There are two types of recursion:
- direct recursion – when we have a call to the same function from the body of that function
- indirect recursion – when we have function A calling function B, calling function C, which in return calls function A again, creating a sort of a ring. These functions are also called mutually recursive.
As with infinite loops, recursive functions also hold the danger of infinite recursion. Whenever you use recursion, you should make sure that you specify at least a case when you get a concrete result, which does not need another recursive call. In other words, at least one case when the recursion is terminated. Programmers call this specific case bottom of recursion. In our previous example, the bottom of recursion is when the n variable reaches a value less than or equal to 2. If you do not specify a bottom of recursion, you will most likely end up with a StackOverflowException.
So, how do we create a recursive function? As with any other programming task, you should divide the task that you are trying to solve into subtasks, for the solution of which we can use the same algorithm, like in a pattern. In the end, the combination of all subtasks should lead to the solution of your initial task. For each subtask, the calculation should be altered in such fashion that at some point, the bottom of recursion is met.
Now that we established that we need a pattern of some sort to be able to create a recursion, lets try another example. And, sorry, math again… This time, we will calculate factorial numbers. What are they? A factorial number n (written n!) is the product of all the integer numbers between 1 and n inclusive. There is a single exception, 0! is by definition 1. At a basic definition, we can write this as:
n! = 1 * 2 * 3 * ... * n
That is the general definition, but how can we identify a pattern which we can use for our recursive implementation? Let’s take the discrete representation of a few of the elements:
0! = 1 1! = 1 = 1 * 1 = 1 * 0! 2! = 2 * 1 = 2 * 1! 3! = 3 * 2 * 1 = 3 * 2! 4! = 4 * 3 * 2 * 1 = 4 * 3! 5! = 5 * 4 * 3 * 2 * 1 = 5 * 4! 6! = 6 * 5 * 4 * 3 * 2 * 1 = 6 * 5!
and so on. And now, we can clearly see that there is the following pattern:
n! = n * (n - 1)!
From this we can say that our bottom of recursion will be the last case of the sequence, n = 0, when the value of the factorial is equal to 1. We are sure that our recursion will not be infinite because for each recursion we calculate n – 1 and multiply the result with n, and the subsequent subtraction of 1 from n will eventually lead to 0, the bottom of our recursion. At this point, we can write the following function:
static void Main(string[] args)
{
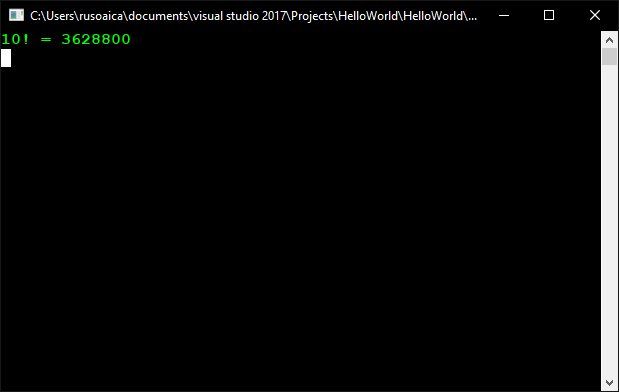
decimal factorial = Factorial(10);
Console.WriteLine("{0}! = {1}", 10, factorial);
Console.Read();
}
static decimal Factorial(int n)
{
if (n == 0) // The bottom of the recursion
return 1;
else // Recursive call: the method calls itself
return n * Factorial(n - 1);
}
and this is how the result will look like:
However, like in our Fibonacci example, this is also a bad implementation of recursion, even though when explaining recursive functions, factorial numbers is the preferred exercise in universities. That is why I will also explain to you the alternative, using iterations, which in this particular case is more efficient. The only difference is that iteration is often not as intuitive as recursion.
static decimal Factorial(int n)
{
decimal result = 1;
for (int i = 1; i <= n; i++)
result = result * i;
return result;
}
What you should remember is that, though recursion is a powerful tool, iteration, when possible, is more efficient. That is why, whenever you can adapt a piece of code to use iteration over recursion, do it. Your program will run faster.
Let’s look at another example where we could use recursion to solve the problem. This time we are going to consider an iterative solution, too. If you remember the nested loops lesson, we had there something like this:
for (a1 = 1; a1 <= K; a1++)
for (a2 = 1; a2 <= K; a2++)
for (a3 = 1; a3 <= K; a3++)
…
for (aN = 1; aN <= K; aN++)
Console.WriteLine("{0} {1} {2} … {N}", a1, a2, a3, …, aN);
The above example is easy to understand, we have nested loops, and they are easy to implement, when we previously know the number of loops we need. But when we don’t, that’s where problems start to arise. If we want to search for a file on hard drive, starting from a root directory, we could use loops for each new level in the directory tree, but only if we would know in advance how deep that tree branches, and how deep our nested loops must go. But we don’t know, which makes it difficult or impossible to implement.
So, trying to break down our problem, we can say that we need a set of instructions for N number of nested loops from 1 to K. As an example, when N = 2 and K = 3 (meaning “two nested loops, from 1 to K), and also when N = 3 and K = 3, this should be the result:
1 1 1 1 1
1 2 1 1 2
1 3 1 1 3
N = 2 2 1 N = 3 1 2 1
K = 3 -> 2 2 K = 3 -> …
2 3 3 2 3
3 1 3 3 1
3 2 3 3 2
3 3 3 3 3
Each row of the result can be regarded as ordered sequence of N numbers. The first one represents the current value of the counter of the loop, the second one – of the second loop, etc. On each position we can have value between 1 and K. The solution of our task boils down to finding all ordered sequences of N elements for N and K given. If we are looking for a recursive solution to the problem, the first problem we are going to face is finding a recurrent dependence. Let’s look more carefully at the example from the assignment and put some further consideration. Notice that, if we have calculated the answer for N = 2, then the answer for N = 3 can be obtained if we put on the first position each of the values of K (in this case from 1 to 3), and on the other two positions we put each of the couples of numbers, produced for N = 2. We can check that this rule applies for numbers greater than 3. This way we have obtained the following dependence – starting from the first position, we put on the current position each of the values from 1 to K and continue recursively with the next position. This goes on until we reach position N, after which we print the obtained result (bottom of the recursion). Here is how the method looks implemented in C#:
static void NestedLoops(int currentLoop)
{
if (currentLoop == numberOfLoops)
{
PrintLoops();
return;
}
for (int counter = 1; counter <= numberOfIterations; counter++)
{
loops[currentLoop] = counter;
NestedLoops(currentLoop + 1);
}
}
We are going to keep the sequence of values in an array called loops, which would be printed on the console by the method PrintLoops() when needed. The method NestedLoops() takes one parameter, indicating the position in which we are going to place values. In the loop we place consecutively on the current position each of the possible values (the variable numberOfIterations contains the value of K entered by the user), after which we call recursively the method NestedLoops() for the next position. The bottom of the recursion is reached when the current position becomes N (the variable numberOfIterations contains the value of N, entered by the user). In this moment we have values on all positions and we print the sequence. Here is a complete implementation of the recursive nested loops solution:
static int numberOfLoops;
static int numberOfIterations;
static int[] loops;
static void Main(string[] args)
{
Console.Write("N = ");
numberOfLoops = int.Parse(Console.ReadLine());
Console.Write("K = ");
numberOfIterations = int.Parse(Console.ReadLine());
loops = new int[numberOfLoops];
NestedLoops(0);
Console.Read();
}
static void NestedLoops(int currentLoop)
{
if (currentLoop == numberOfLoops)
{
PrintLoops();
return;
}
for (int counter = 1; counter <= numberOfIterations; counter++)
{
loops[currentLoop] = counter;
NestedLoops(currentLoop + 1);
}
}
static void PrintLoops()
{
for (int i = 0; i < numberOfLoops; i++)
Console.Write("{0} ", loops[i]);
Console.WriteLine();
}
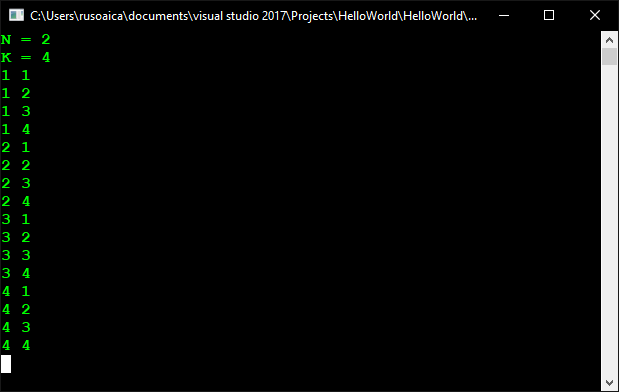
If we run the application and enter for N and K respectively 2 and 4 as follows, we are going to obtain the following result:
In the Main() method we enter values for N and K, create an array in which we are going to keep the sequence of values, after which we call the method NestedLoops(), starting from the first position. Notice that as a parameter of the array we give 0 because we keep the sequence of values in an array, and as we already know, counting of array elements starts from 0. The method PrintLoops() iterates all elements of the array and prints them on the console.
Now that we saw how nested loops look like using recursion, lets have a look at the second way of implementing the nested loops, iteration. For the implementation of an iterative solution of the nested loops we can use the following algorithm, which finds the next sequence of numbers and prints it at each iteration:
- In the beginning on each position place the number 1.
- Print the current sequence of numbers.
- Increment with 1 the number on position N. If the obtained value is greater than K replace it with 1 and increment with 1 the value on position N – 1. If its value has become greater than K, too, replace it with 1 and increment with 1 the value on position N – 2, etc.
- If the value on the first position has become greater than K, the algorithm ends its work.
- Go on with step 2.
Below we propose a straightforward implementation of the described iterative nested loops algorithm:
static int numberOfLoops;
static int numberOfIterations;
static int[] loops;
static void Main(string[] args)
{
Console.Write("N = ");
numberOfLoops = int.Parse(Console.ReadLine());
Console.Write("K = ");
numberOfIterations = int.Parse(Console.ReadLine());
loops = new int[numberOfLoops];
NestedLoops();
Console.Read();
}
static void NestedLoops()
{
InitLoops();
int currentPosition;
while (true)
{
PrintLoops();
currentPosition = numberOfLoops - 1;
loops[currentPosition] = loops[currentPosition] + 1;
while (loops[currentPosition] > numberOfIterations)
{
loops[currentPosition] = 1;
currentPosition--;
if (currentPosition < 0)
return;
loops[currentPosition] = loops[currentPosition] + 1;
}
}
}
static void InitLoops()
{
for (int i = 0; i < numberOfLoops; i++)
loops[i] = 1;
}
static void PrintLoops()
{
for (int i = 0; i < numberOfLoops; i++)
Console.Write("{0} ", loops[i]);
Console.WriteLine();
}
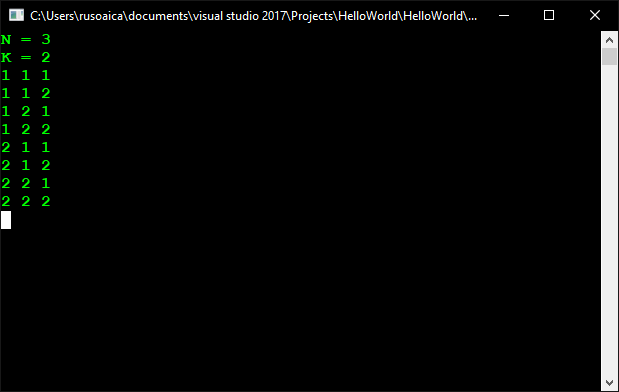
The methods Main() and PrintLoops() are the same as in the implementation of the recursive solution. The NestedLoops() method is different. It now implements the algorithm for iterative solution of the problem and for this reason does not get any parameters, unlike in the recursive version. In the very beginning of this method we call the method InitLoops(), which iterates the elements of the array and places in each position 1. The steps of the algorithm we perform in an infinite loop, from which we are going to escape in an appropriate moment by ending the execution of the methods via the operator return. The way we implement step 3 of the algorithm is very interesting. The verification of the values greater than K, their substitution with 1 and the incrementing with 1 the value on the previous position (after which we make the same verification for it too) we implement by using one while loop, which we enter only if the value is greater than K. For this purpose, we first replace the value of the current position with 1. After that the position before it becomes current. Next, we increment the value on the new position with 1 and go back to the beginning of the loop. These actions continue until the value on the current position is not less than or equal to K (the variable numberOfIterations contains the value of K), which is when we escape the loop. When the value on the first position becomes greater than K (this is the moment when we have to end the execution), on its place we put 1 and try to increment the value on the previous position. In this moment the value of the variable currentPosition becomes negative (as the first position of the array is 0) and we end the execution of the method using the operator return. This is the end of our task. We can now test it with N = 3 and K = 2, for example:
So, in the end, which is better? Iteration or recursion?
If the algorithm solving of the problem is recursive, the implementation of recursive solution can be much more readable and elegant than iterative solution to the same problem.Sometimes defining equivalent algorithm is considerably more difficult and it is not easy to be proven that the two algorithms are equivalent. In certain cases by using recursion we can accomplish much simpler, shorter and easy to understand solutions. On the other hand, recursive calls can consume much more resources (CPU time and memory). In certain situations the recursive solutions can be much more difficult to understand and follow than the relevant iterative solutions. Recursion is powerful programming technique, but we have to think carefully before using it. If used incorrectly, it can lead to inefficient and tough to understand and maintain solutions.
I said at the beginning of this long lesson that I will further explain why the Fibonacci’s number example is inefficient. If we set in our example the value of n = 100, the calculations would take so much time that no one would wait to see the result. The reason is that similar implementation is extremely inefficient. Each recursive call leads to two more calls and each of these calls causes two more calls and so on. That’s why the tree of calls
grows exponentially as shown on the figure below. The count of steps for computing of fib(100) is of the order of 1.6 raised to the power 100 (this could be mathematically proven), whereas, if the solution is linear, the count of steps would be only 100. The problem comes from the fact that there are a lot of excessive
calculations. You can notice that fib(2) appears below many times on the Fibonacci tree:
Now, lets talk a bit about the correct implementation of such a recursive solution. We can optimize the recursive method for calculating the Fibonacci numbers by remembering (saving) the already calculated numbers in an array and making recursive call only if the number we are trying to calculate has not been calculated yet. Thanks to this small optimization technique (also known in computer science and dynamic optimization as memoization (not to be confused with memorization) the recursive solution would work for linear count of steps. Here is a sample implementation:
static long[] numbers;
static void Main(string[] args)
{
Console.Write("n = ");
int n = int.Parse(Console.ReadLine());
numbers = new long[n + 2];
numbers[1] = 1;
numbers[2] = 1;
long result = Fib(n);
Console.WriteLine("fib({0}) = {1}", n, result);
Console.Read();
}
static long Fib(int n)
{
if (0 == numbers[n])
numbers[n] = Fib(n - 1) + Fib(n - 2);
return numbers[n];
}
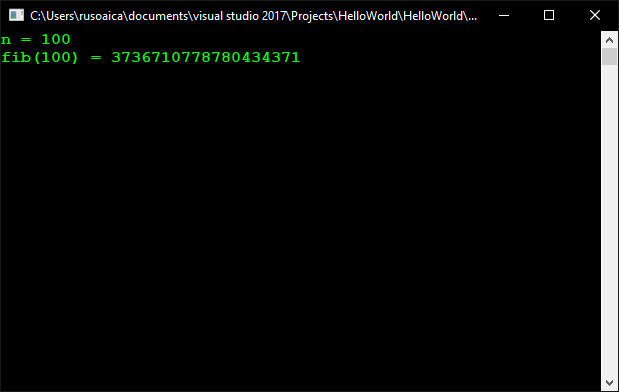
Do you notice the difference? While with the initial version if n = 100 it seems like the computation goes on forever, with the optimized solution we get an answer instantly. As we will learn later, the first solution runs in exponential time while the second is linear:
We can even improve upon the previous concept of retaining the previous numbers values. It is not hard to notice that we can solve the problem without using recursion, by calculating the Fibonacci numbers consecutively. For this purpose we are going to keep only the last two calculated elements of the sequence and use them to get the next element. Bellow you can see an implementation of the iterative Fibonacci numbers calculation algorithm:
static void Main(string[] args)
{
Console.Write("n = ");
int n = int.Parse(Console.ReadLine());
long result = Fib(n);
Console.WriteLine("fib({0}) = {1}", n, result);
Console.Read();
}
static long Fib(int n)
{
long fn = 0;
long fnMinus1 = 1;
long fnMinus2 = 1;
for (int i = 2; i < n; i++)
{
fn = fnMinus1 + fnMinus2;
fnMinus2 = fnMinus1;
fnMinus1 = fn;
}
return fn;
}
This solution is not only short and elegant, but also hides the risks of using recursion. Besides, it is efficient and does not require extra memory. Concluding the previous examples I can give you the next recommendation:
Avoid recursion, unless you are certain about how it works and what has to happen behind the scenes. Recursion is a great and powerful weapon, with which you can easily also shoot yourself in the leg (ouch!). Use it carefully!
To conclude this lesson, lets see an example which I already suggested, searching for a file in a directory, with subdirectories:
using System;
using System.IO;
namespace HelloWorld
{
class Program
{
static void Main(string[] args)
{
Console.Read();
DirSearch(@"C:\", "test.txt");
}
static void DirSearch(string searchRootDirectory, string searchFileName)
{
try
{
foreach (string directory in Directory.GetDirectories(searchRootDirectory))
{
foreach (string file in Directory.GetFiles(directory, searchFileName))
{
Console.WriteLine(file);
}
DirSearch(directory, searchFileName);
}
}
catch (System.Exception excpt)
{
Console.WriteLine(excpt.Message);
}
}
}
}
In the above code, there are a few new things I haven’t talked yet, like the try…catch instruction, and you should ignore it. You will understand it better when the time comes. You should also notice that I used the using System.IO; instruction, because we are using functions such as Directory.GetDirectories(), which reside in the System.IO assembly. Do not worry about them either, for now. All that is left for me to specify is that, though we not learned about them yet, Directory.GetDirectories() and Directory.GetFiles() do just that: they return a list of directories, respectively files, from a certain path we specify. So, as we learned in the lesson iteration of array elements, we are using a Foreach loop to go through all the elements of the list returned by the Directory.GetDirectories() instruction. Then, for each of these directory, we are using another Foreach loop, to iterate through the list of all files that match certain criteria, contained in that directory, list provided by Directory.GetFiles(). This is the place where we actually print the found files on the console. However, what makes this method recursive is the fact that on each iteration of the Foreach loop that goes through the directories, we are calling the DirSearch() method again, with the current directory that is iterated. This means that the current loop will wait until this new call to the method is completed, and only then will resume its cycling. Of course, if in the new call to the method Directory.GetFiles() will contain a new list of directories (subdirectories of the directory we used in first loop, when we called the method), the foreach loop will again call the function again, for each of these directories, and so on. This means that if we have a tree of directories, the function will recursively go through all of them.
Tags: functions, recursive functions

lol @ “Concluding (…) I can give you the next recommendation: Avoid recursion”. 😉
Until you will reach an example where without using it, you will be banging your head against the walls for days… 😉