Finally, we now know enough to start talking about LINQ, which is an acronym for Language Integrated Query which is basically just a fancy way of doing queries and SQL-like things in C#. If you don’t know what SQL is, you should probably research about it a bit first, but, at a macro level, SQL (Structured Query Language) is just a language for interacting with databases. In our case, LINQ is used for the same macro concept: interacting with collections of data, directly in memory, using only C#, with strong type support.
What does strong type mean? Well, assuming you have the slightest idea about SQL, the basic syntax for selecting some numeric values which are less than a certain value from a database table named Numbers (…duh!) is this one: SELECT number FROM Numbers WHERE number < 5;. In C#, we would be forced to write that SQL query, that syntax, using a string variable, something like this:
[raw]
[/raw]
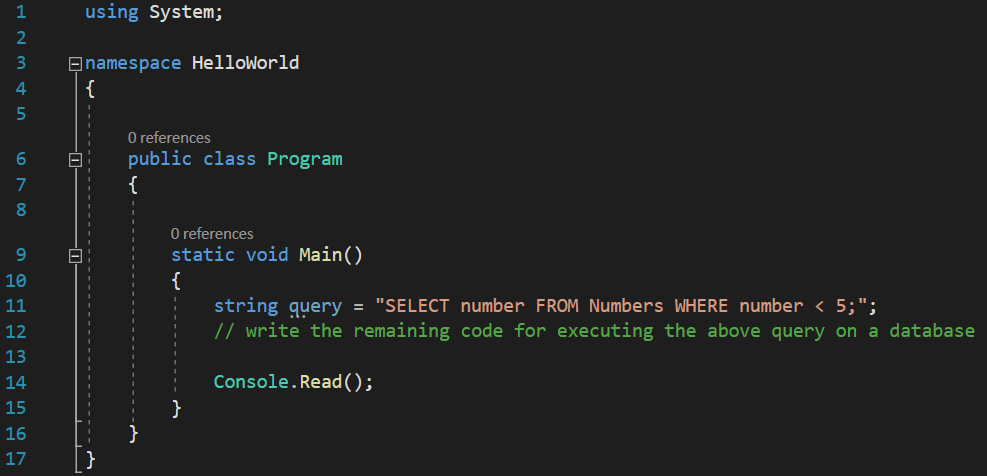
The problem with this approach is the fact that we are using a string. Strings are prone to errors, we can at any time mistype a letter and the compiler would give us no error. If we typed Number instead of Numbers, why would the compiler show us an error? For it, it is a simple string, and it is a valid syntax. It does not understand that we intend it as a query, an SQL statement that does something on a database. For all it cares, it could just as well be a paragraph from a Sci-Fi novel. And if you ever decide to rename your database table, good luck hunting all the query strings in your application, to update them with the new name!
What would be wonderful is for us to use variables, types and the C# language in general for the query itself, such that if we mistyped something, an error would show up. That would be the above mentioned strong typing, we would be using the constructs of the language itself to write our query, and not declare it as a string. Fortunately, this is exactly what LINQ was designed for.
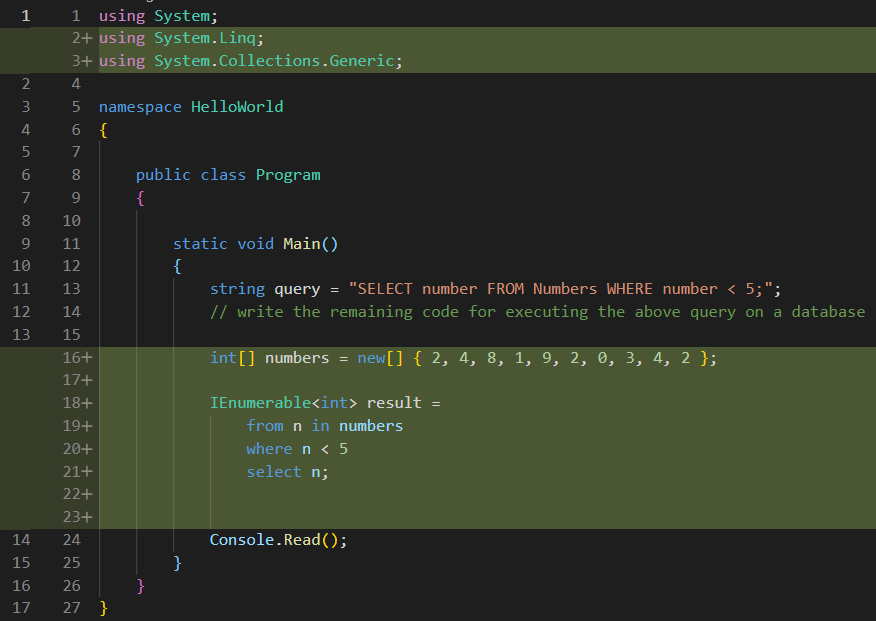
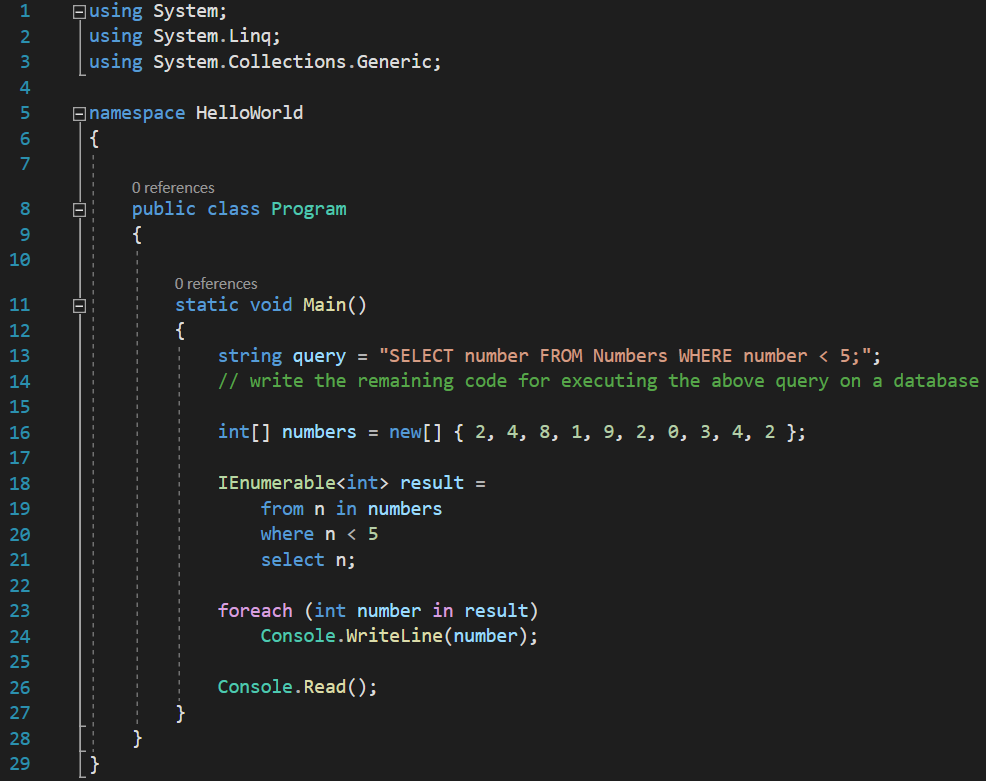
For the sake of simplicity, we will not be using a real database to get our data, instead, we will declare a simple int array and pretend it is a database table:
See code changes
Legend:
[/raw]

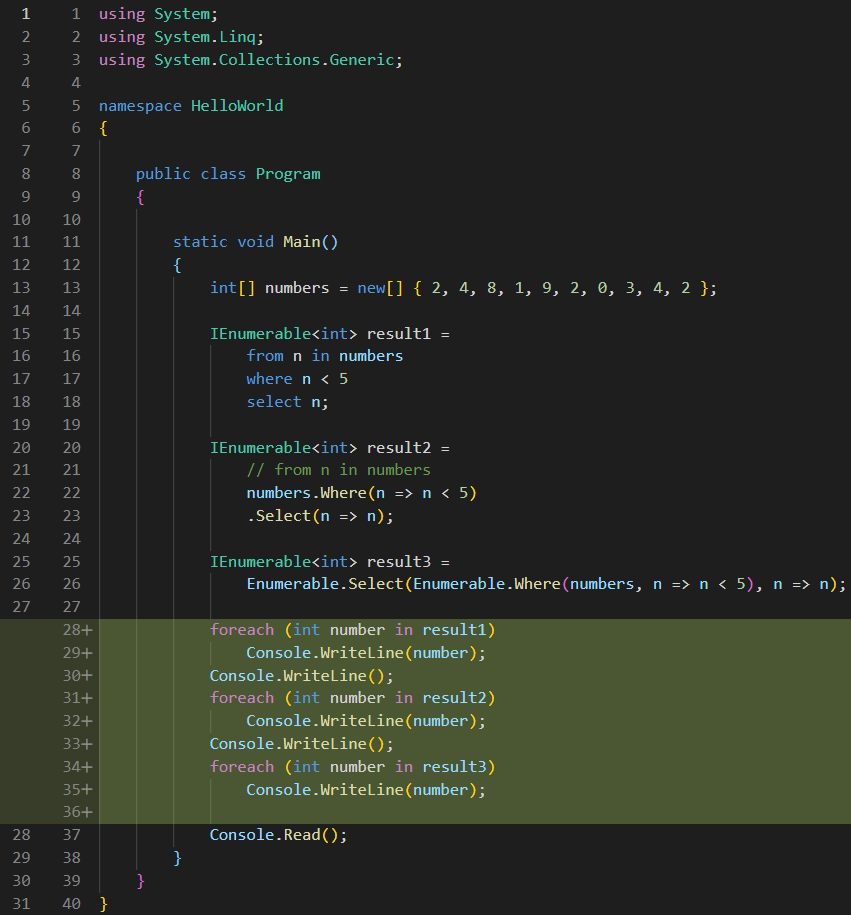
The above syntax, in which we declare a variable named result, of type IEnumerable, and we assigned a weird syntax to it, is the direct C# translation of the initial string query, and it was written with the help of LINQ. You can figure this out because of the using System.Linq; statement added at the top of the file: if you remove that line, you will get a compiler error, because, obviously, what I wrote above is not valid syntax that can be directly converted to MSIL. It involves a ton of syntactic sugar that the compiler has to desugarize.
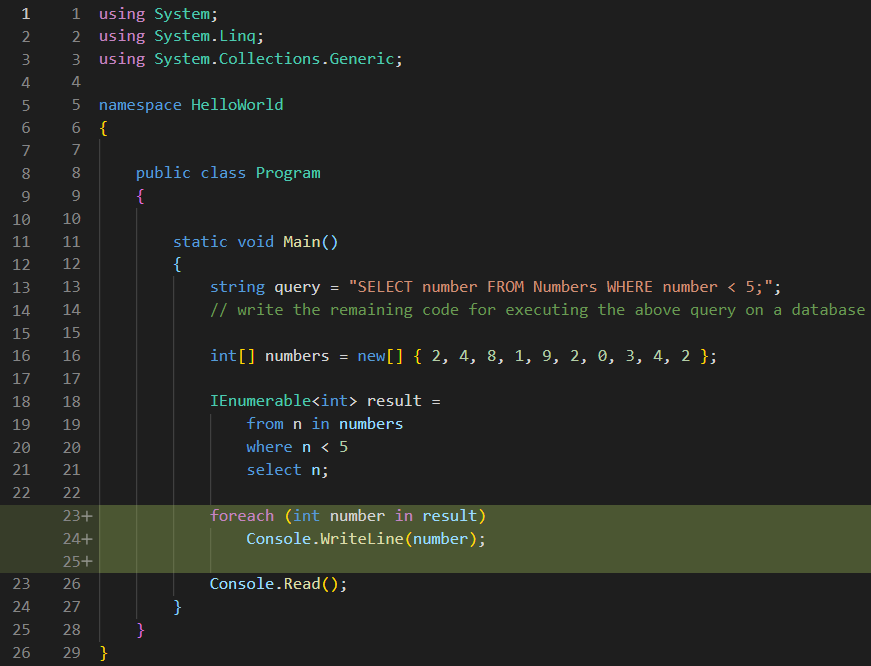
Anyway, for now, just have a look at the syntax and observe the fact that it does not resemble any C# language we used so far. There is no dot anywhere, there is no methods call, but we can see that it produces a result of type IEnumerable<int>. This is called free form syntax, or, as Microsoft puts it, declarative query syntax. But the above syntax is intuitive enough to get its basic idea: “for each number n in numbers, select n where n is less than 5, and put the results in an IEnumerable”. And if it’s an IEnumerable, that means we can iterate through the results and display them at the console:
See code changes
Legend:
[/raw]
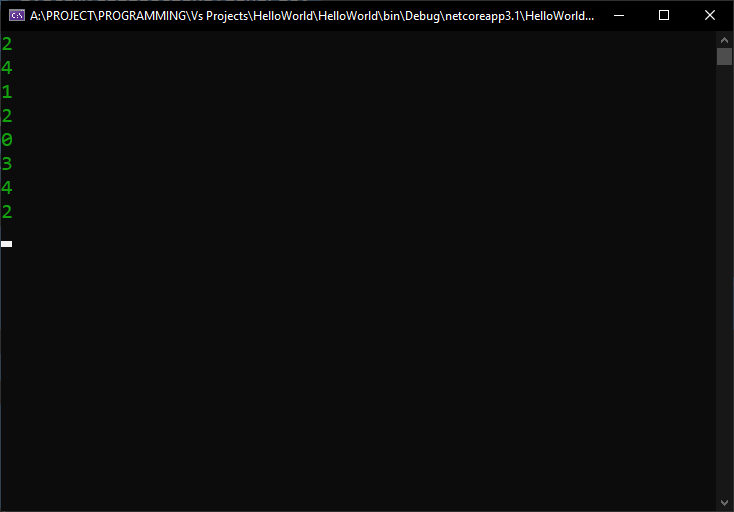
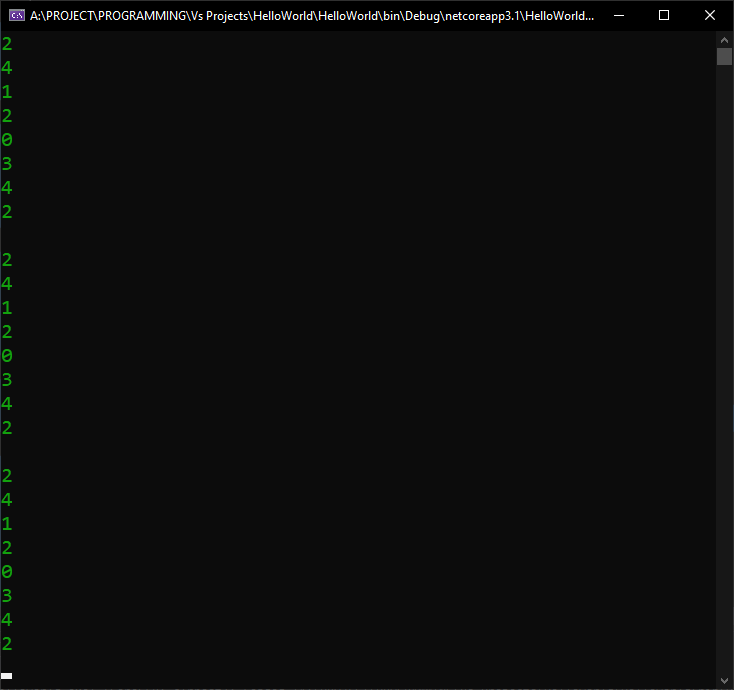
And from the result, we can see that, yes, the numbers are indeed filtered the way we wanted:
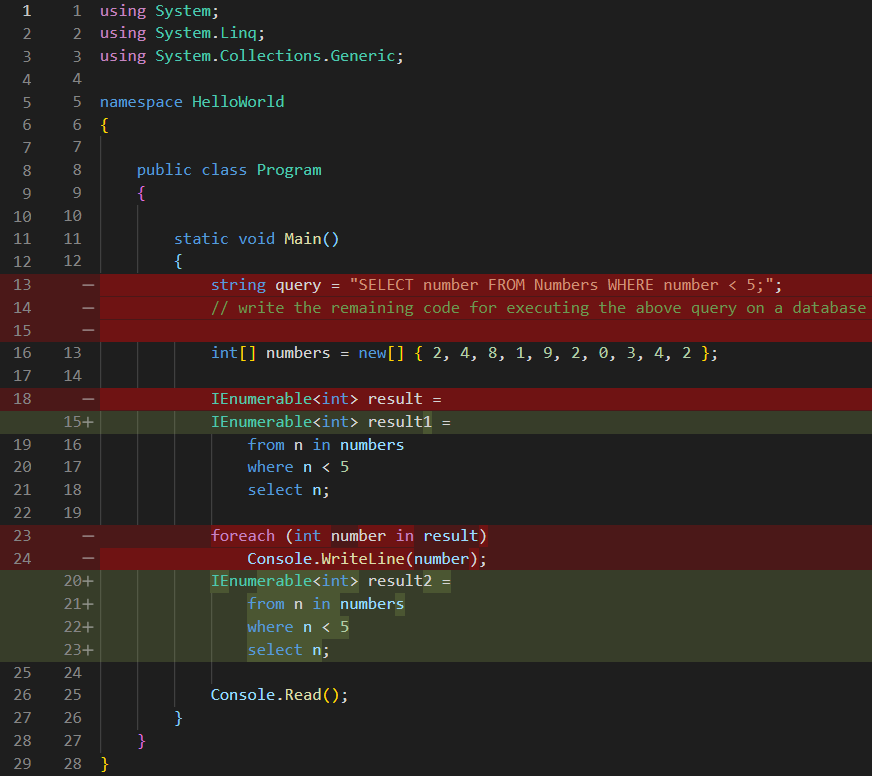
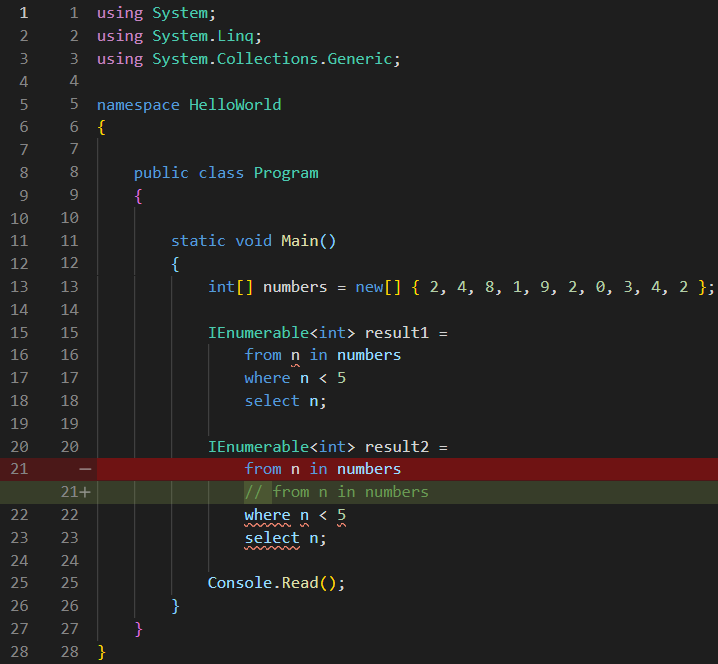
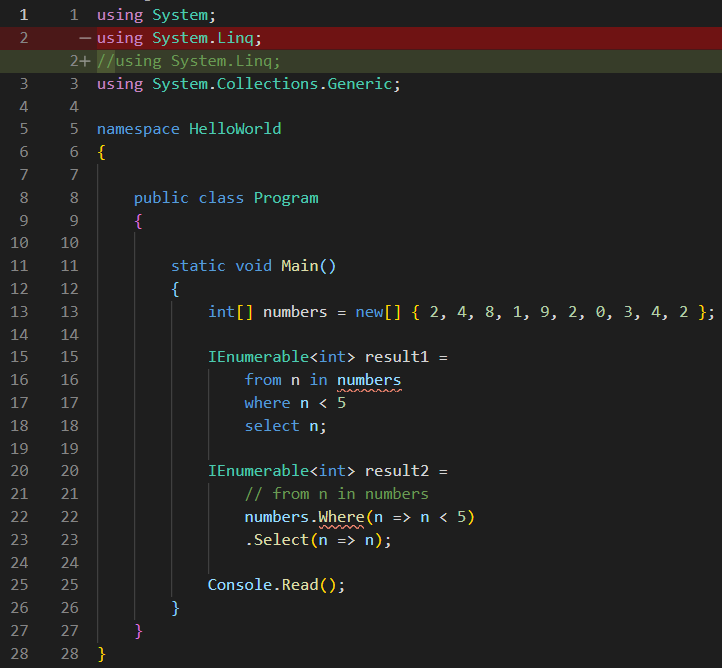
Now, let’s analyze what the compiler has to do with this free form syntax, since I already said it is not even close to valid MSIL code. So, I will rename the result variable to result1, then I will copy it to a new variable and name it result2, then I will convert result2 to what the compiler would do, step by step:
See code changes
Legend:
[/raw]
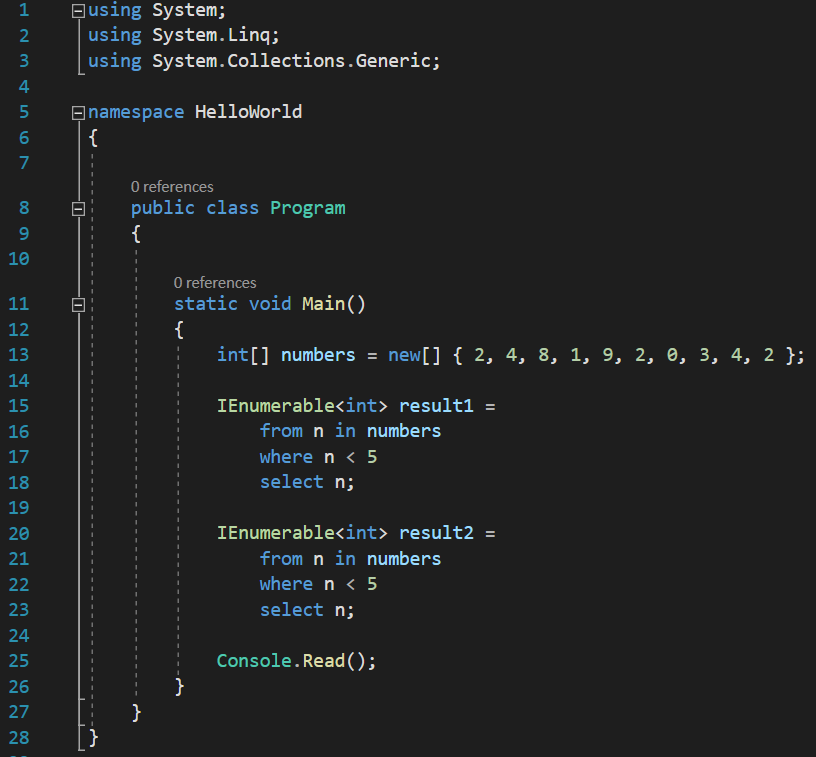
So, the first step that the compiler does is to look at this code: from n in numbers, and it doesn’t translate it to anything, it just discards it. It just analyses it and from it, it just takes two things: a data source called numbers and a variable called n. I will discard this line too:
See code changes
Legend:
[/raw]

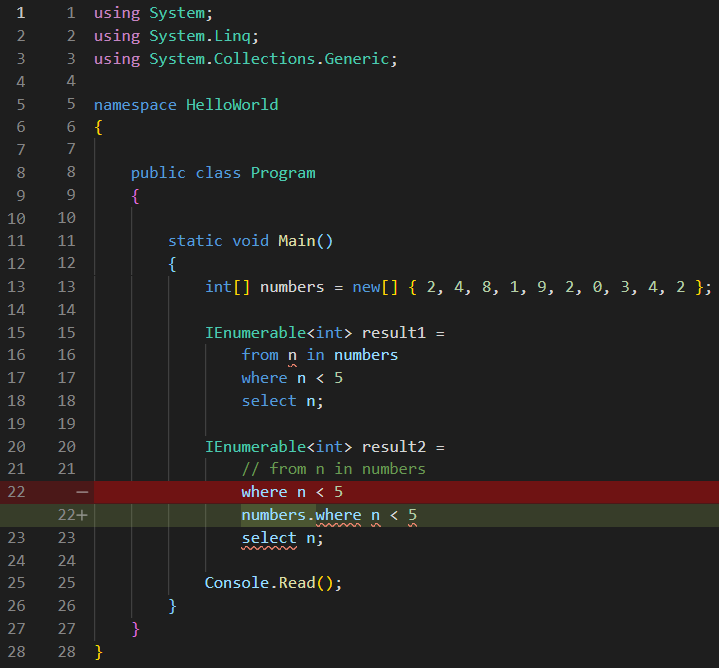
Obviously, at this point, I no longer have a valid syntax, and I will get a few compiler errors. But, regardless, the compiler will get to the next step, which is defining the source of the data that it will use (the source that it took from the discarded line), and add a dot after it:
See code changes
Legend:
[/raw]
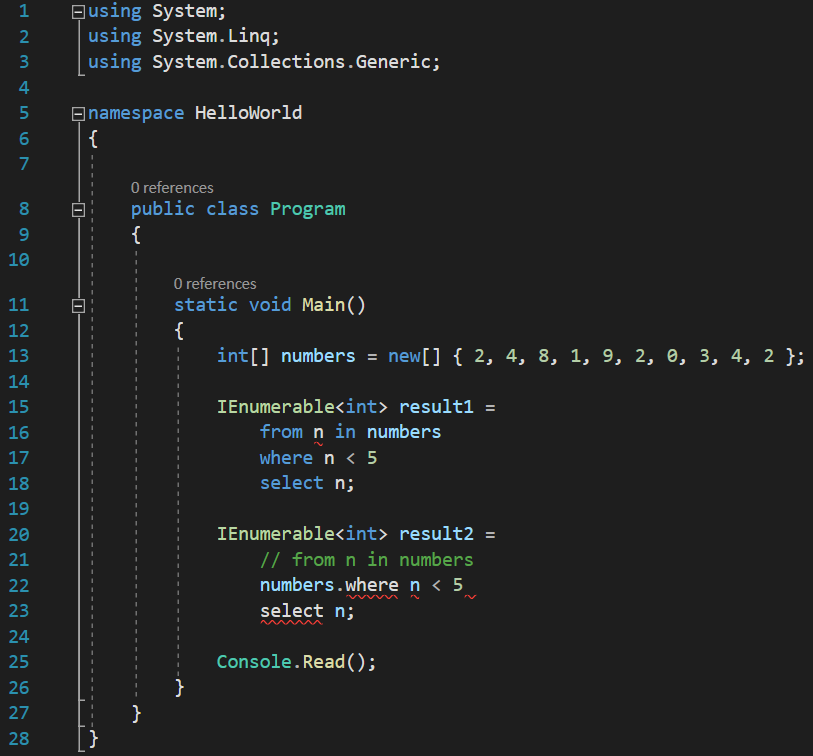
Finally! A dot! We’re starting to feel like programmers again!
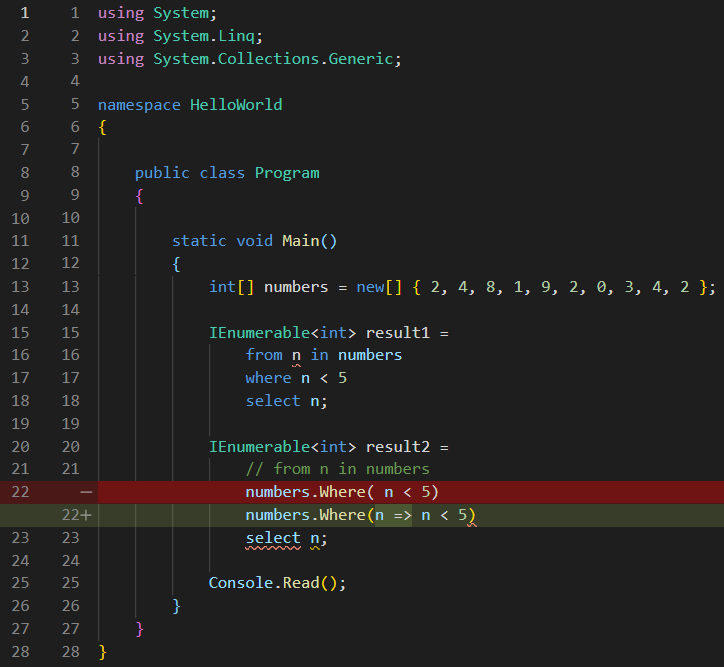
Next, the compiler doesn’t really look at what where means, it just replaces it with an uppercase Where, just like any other method name in C#. Of course, if it is going to treat it as a method, it also needs to add some parenthesis, to invoke it:
See code changes
Legend:
[/raw]

Now, it needs to know where the n parameter will be taken from. And it will take it from the same first line that it discarded, and convert the whole thing to a lambda expression:
See code changes
Legend:
[/raw]
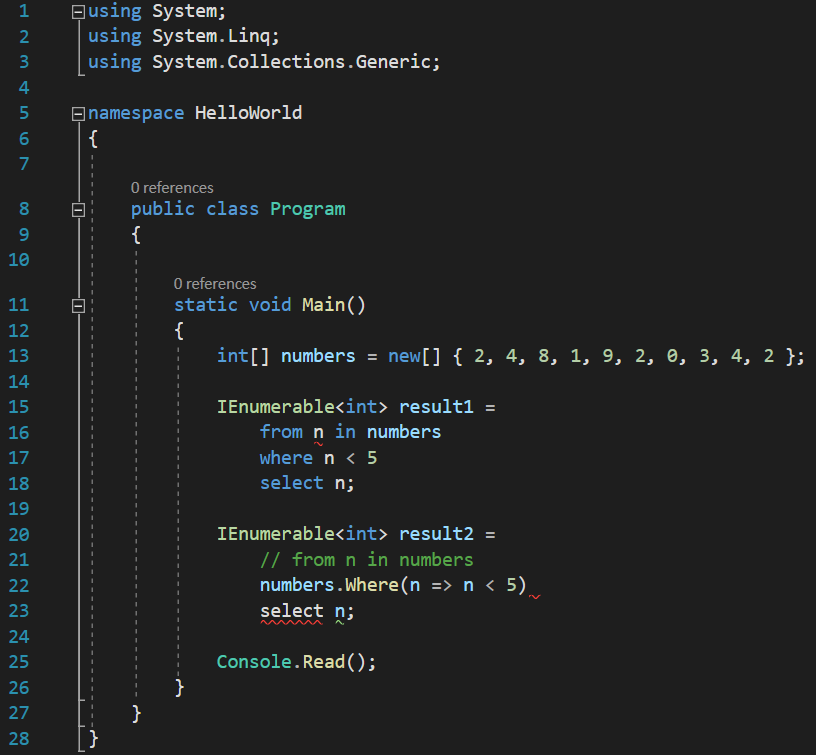
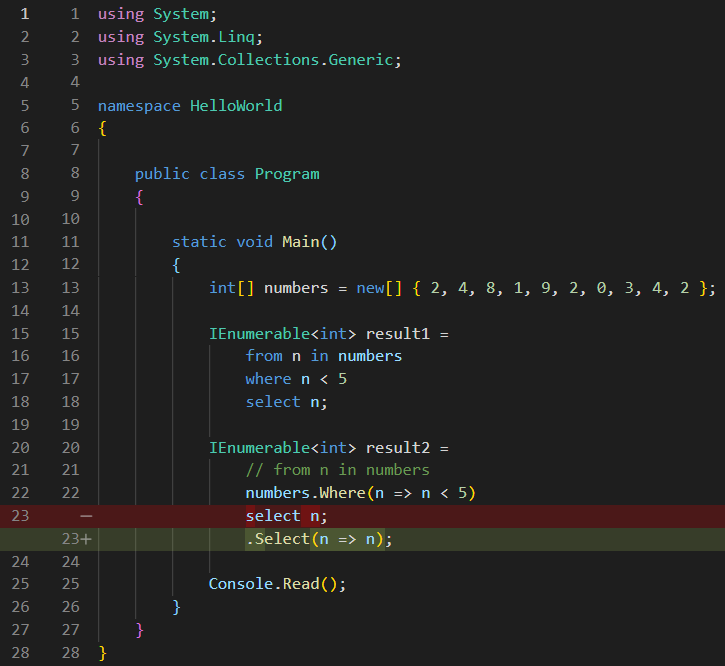
Now, it sees the select, and will say “sure, I understand select!”, and do the same thing it did with the where:
See code changes
Legend:
[/raw]
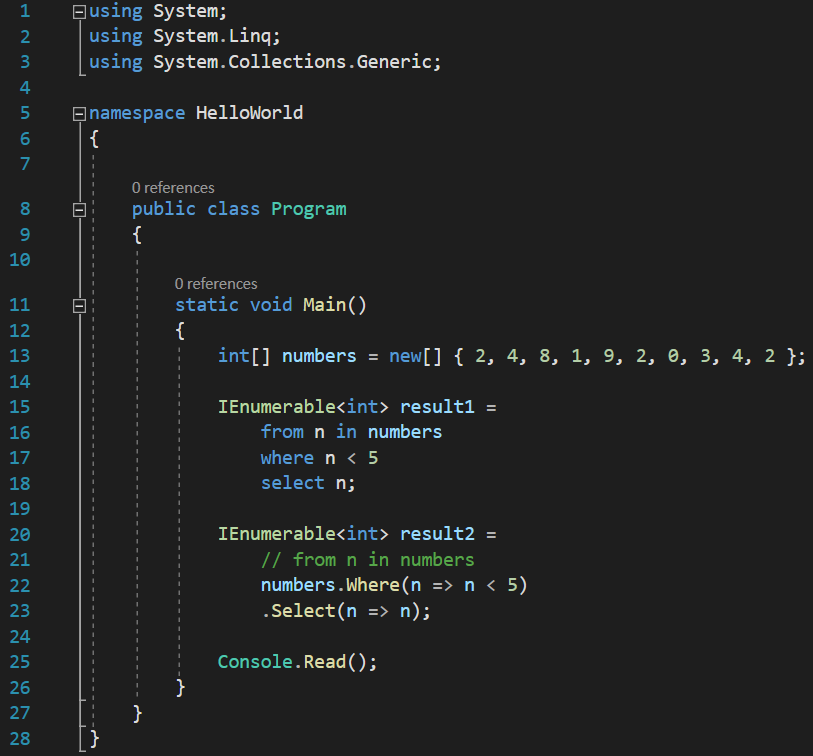
And now, all the compiler errors are gone, and if we display the elements of result2 at the console, we will end up with the same filtered numbers we originally had. You might be thinking that we solved the problem, this should be valid MSIL code, since we are using dots and call methods and yada, yada. But it’s not. If we look at numbers, we see that it is an int array. Well, last time I checked, there was no Where() method on any kind of array. And to prove this, I’m going to comment the using System.Linq; line:
See code changes
Legend:
[/raw]
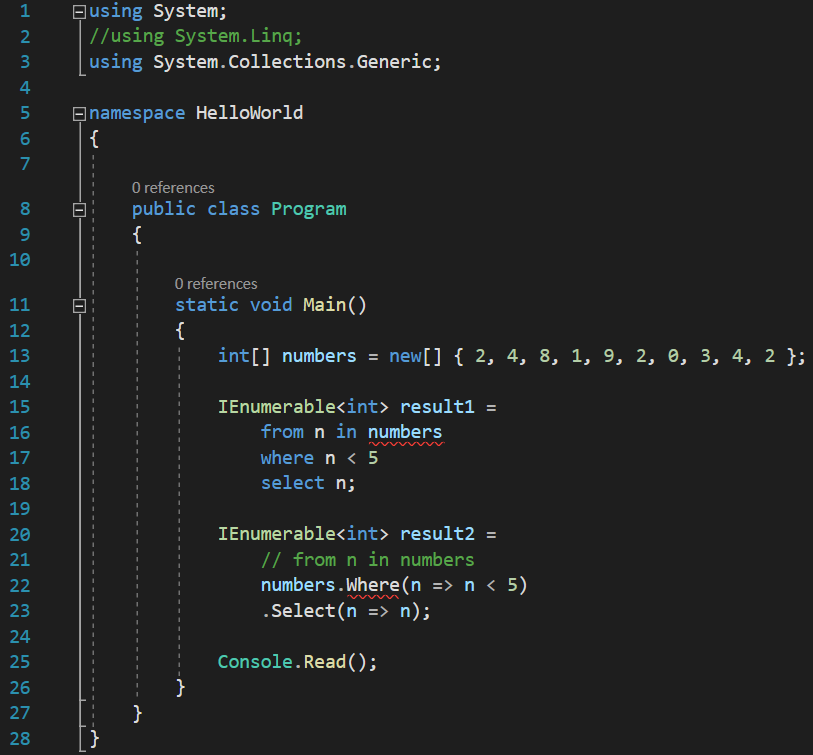
Now, you can see that we get compiler errors not only on the Where() method call, but even for the numbers variable in the declarative syntax:
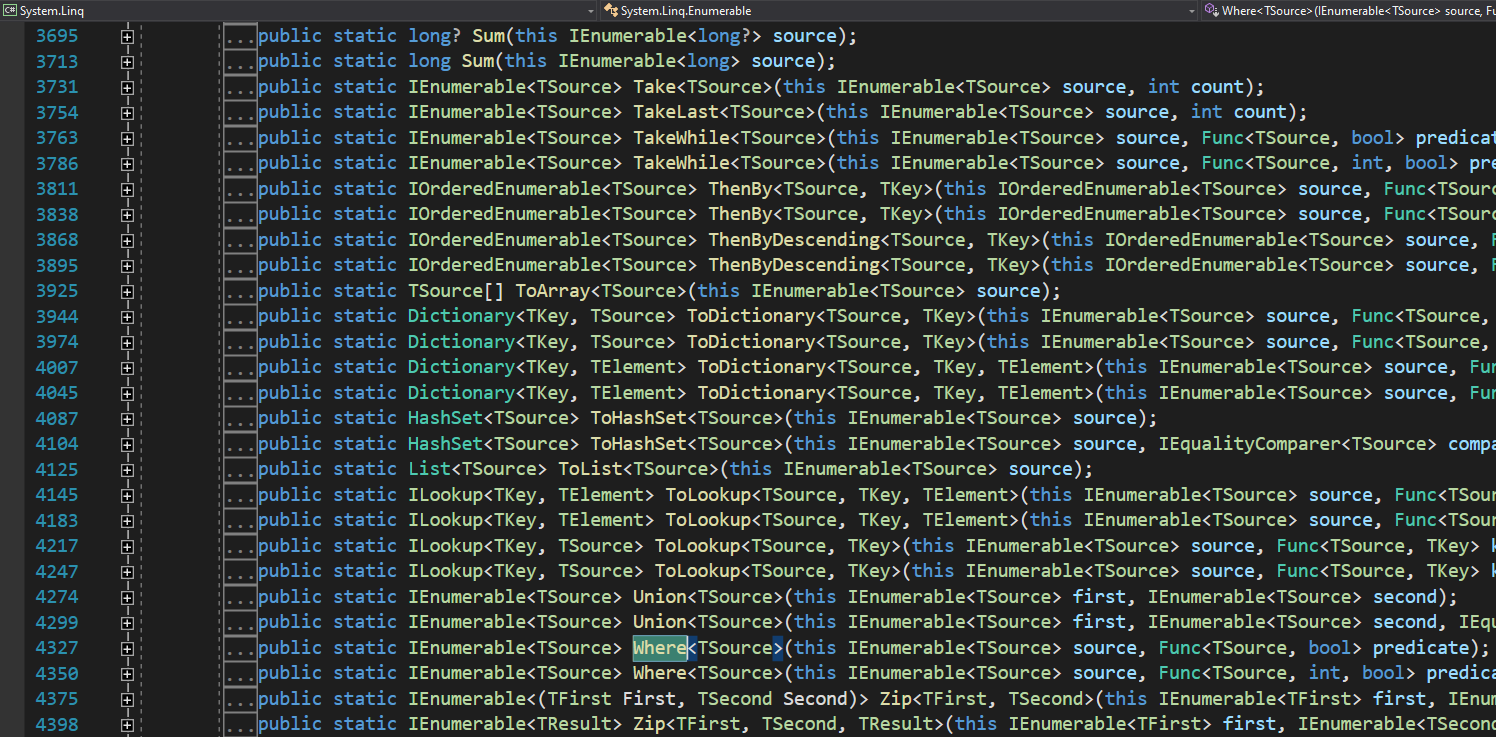
The important concept to take from the above error is “and no accessible extension method”. If I put back the using System.Linq; line, the errors go away, so there must be some extension method inside the System.Linq namespace that extends an array and is named Where(). We can check that out by right clicking on the Where() method and chosing Go To Definition, or pressing the F12 key, and we will see this:
The Where() function returns an IEnumerable, we see that it is an extension method because the first parameter it takes is prefixed with the this keyword, and we see that it extends IEnumerable! If we look at the definition of an array, we see that it also implements the IEnumerable interface too:
Of course, the Where() function is a generic function, and since we are calling it on an int array, the TSource argument will be an int. Then, we see that it takes as second parameter a Func. If you remember, Func is a generic delegate that takes something and returns something: it takes in a T, which in our case is an int, and it’s returning a TResult, which we can see it is a bool, rightfully named predicate, because we are going to predicate on some booleans:
So, what does it actually happen when the compiler calls this Where() function? It will send each one of the ints inside the numbers array one by one to the Func, which is the lambda expression we have inside the parenthesis of the Where() call, and it will run them through the Func: 2 < 5, 4 < 5, 8 < 5, and so on, and so forth. Because Where() also returns an IEnumerable, we can also put a dot after it and call Select(), because, if we look at the signature of the Select() function, we see this:
Would you look at that! Select() is also an extension method for IEnumerable, and also returns an IEnumerable! This means that we can chain these functions and call them one after the other because they both extend IEnumerable, and they both return IEnumerable. And this is really nice: we have the Where() function that filters some numbers, and then we have the Select() function that does something else on those filtered numbers, and so on. We basically have a sort of a pipe that takes something, processes it and sends it further to another pipe.
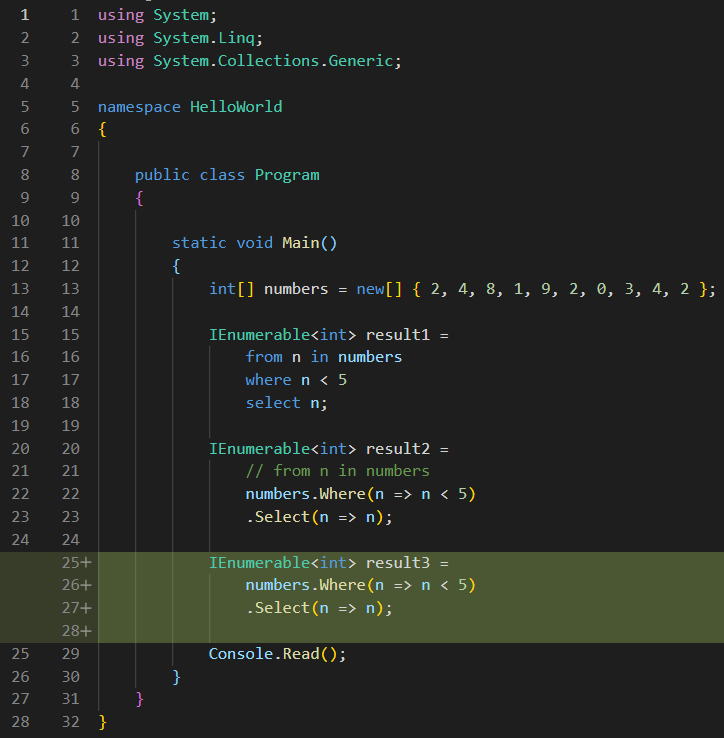
So, this is the first step that the compiler does in translating the free form syntax we had initially. But, if you remember from the extension methods lesson, I said there that extension methods are still invalid MSIL code, they still represent syntactic sugar that the compiler has to desugarize. So, let’s do just that, and let’s convert the extension methods to what the compiler ends up with. For this, I will make yet another copy of the query and put it in a variable named result3:
See code changes
Legend:
[/raw]

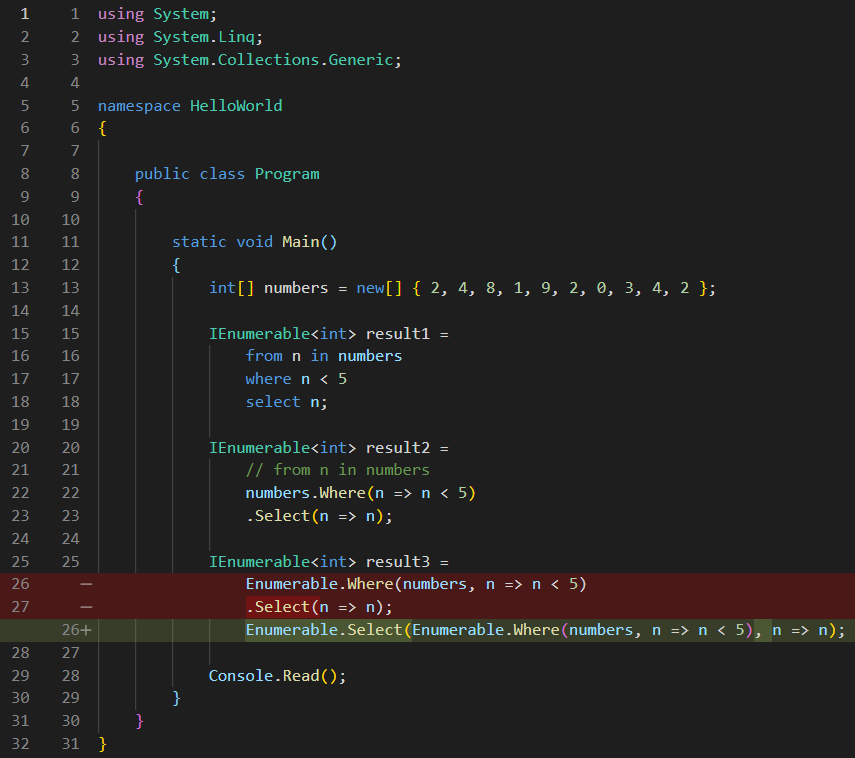
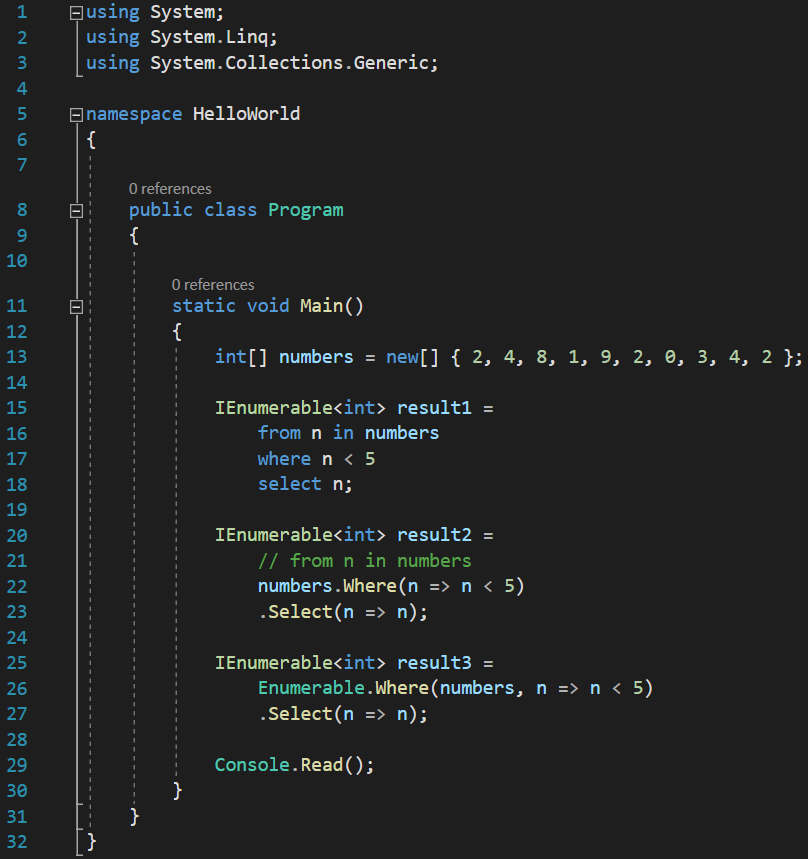
The first step will be for the compiler to take the numbers variable and paste it as the first argument to the Where() function, and then explicitly call the Where() function from the class it is declared in. If we look, we see that it is declared inside a static class named Enumerable .
Be careful and don’t mix up IEnumerable with Enumerable. IEnumerable is an interface, and Enumerable is a class that contains a bunch of extension methods for the IEnumerable interface.
So, let’s do the same first step too:
See code changes
Legend:
[/raw]
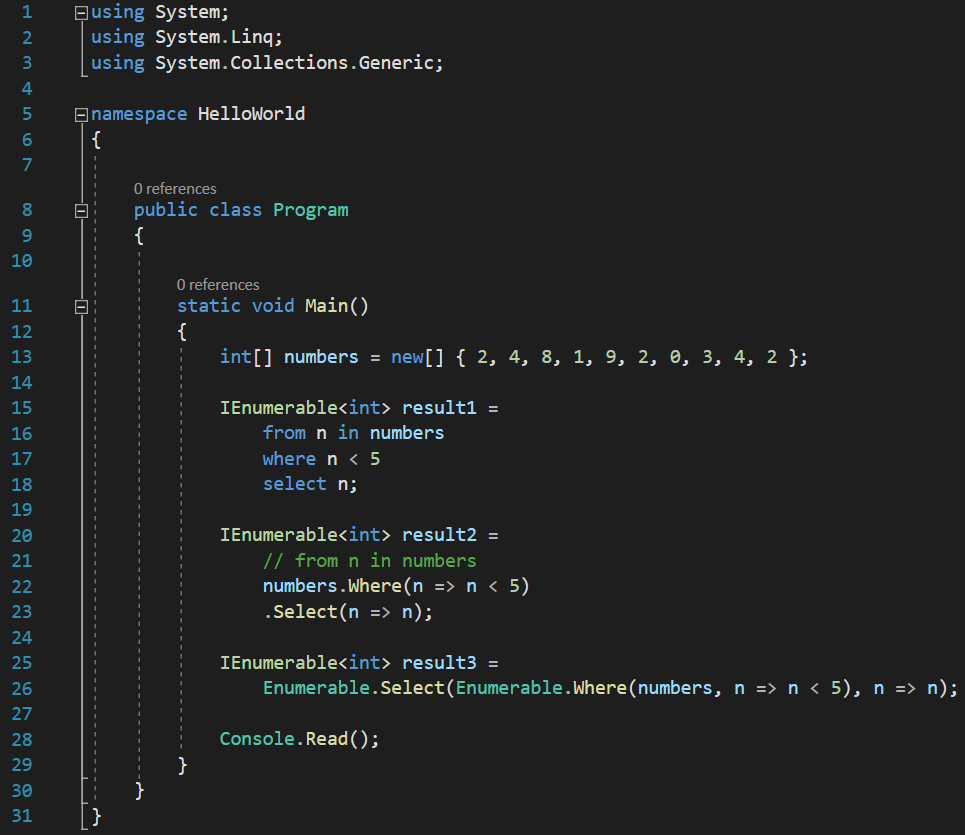
But, at this point, the whole Enumerable.Where() line returns an IEnumerable, which is extended again by Select(), it provides the parameters for the Select(). So, in order to convert Select() too, again, I have to cut the whole Where line and paste it as the first argument to the Select() function, and then explicitly call it too, from the Enumerable class:
See code changes
Legend:
[/raw]
Not even at this point do we have valid MSIL code, because of the lambda expressions, which we know that the compiler has to convert to actual methods inside the class, but except that, this is valid CLR code, this is just static methods calls. And we can iterate all three results, and see they all produce the same values:
See code changes
Legend:
[/raw]
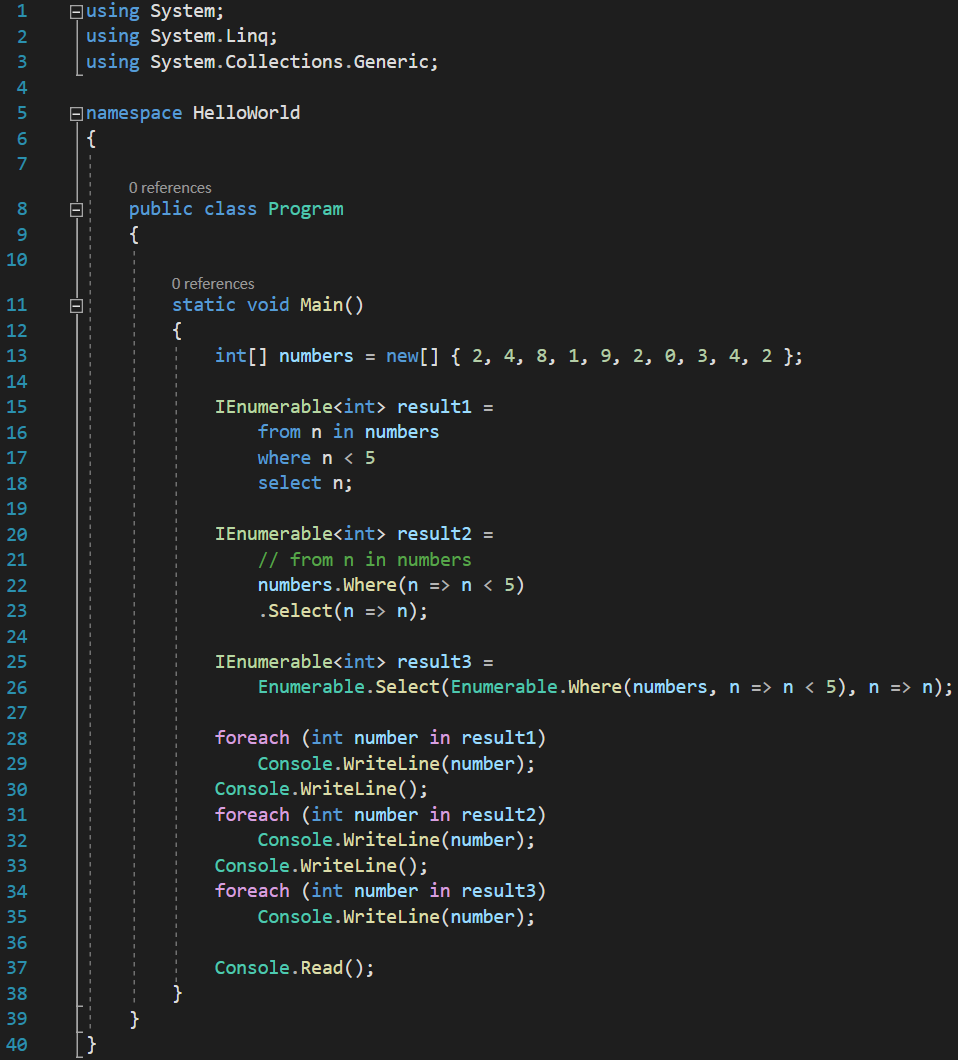
With these results:
Of course, there are tons of other stuff that we need to learn about LINQ in the next lessons, but now we know what LINQ looks like and what it actually is, behind the curtains.
Tags: Enumerable, extension methods, IEnumerable, lambda expression, linq