Explicam într-o lecție anterioară faptul că, la cel mai adânc nivel, computerele stochează și procesează informațiile doar ca două valori, 0 și 1. Aceste valori sunt cele mai mici bucăți individuale de informații din interiorul unui computer, și se numesc biți. Un bit poate conține doar o singură valoare la un moment dat, fie 0 sau 1. Un grup de opt biți se numește byte, octet și, uneori, cuvânt (word). Un octet este cea mai mică bucată de memorie pe care un computer o poate manipula direct. Este de asemenea egal cu un singur caracter, sau o literă. Deci, atunci când tastăm litera A, știm acum că aceasta necesită 1 octet sau 8 biți pentru a fi stocată în memorie.
Ultimul aspect al acestei lecții este de obicei mai greu de înțeles, mai ales de către începători. Cu toate acestea, acest subiect nu este obligatoriu să fie învățat, puteți fi programatori buni chiar și fără să știți să înumărați în mod direct în cod binar.
Dacă vă amintiți din lecțiile de matematică, numărarea binară, numită și numărarea în baza 2, numără doar două valori, 0 și 1. Conform aceluiași principiu, numărătoarea zecimală, numită și numărarea în baza 10, numără 10 valori, de la 0 la 9. Deci, putem spune că în sistemul zecimal începem de la 0, iar limita superioară este 9, după care trebuie să adăugăm o nouă unitate la următoarea magnitudine. Similiar, în sistemul binar, începem să numărăm de la 0, iar limita superioară este 1, după care trebuie să adăugăm o unitate nouă la o magnitudine mai mare. Numărarea binară este într-adevăr aceeași ca și numărarea zecimală, singura diferență fiind folosirea numai a primelor două cifre din aceasta.
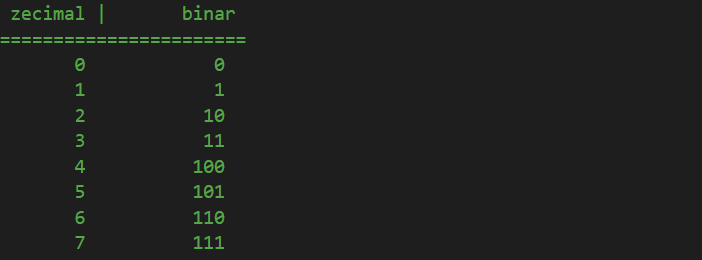
Așadar, vom începe să numărăm atât în sistem binar, cât și în zecimal, pentru comparație. În ambele sisteme, începem cu 0:
Următorul număr în ambele sisteme este 1:
Aici, asemănările se termină. În sistemul zecimal, următorul număr după 1 este 2. Cu toate acestea, deoarece nu există valoarea 2 în binar, pentru că sistemul se termină la 1, putem considera că ajungând la 1 în binar (ultimul număr unitar în binar) este același lucru cu ajungerea la 9 în zecimal (ultimul număr unitar în zecimal). Când vom ajunge la 9 în zecimal, vom adăuga o unitate la următoarea magnitudine superioară și vom începe din nou să înumărăm unitățile de la 0. Cu alte cuvinte, în zecimal, după 9, avem 10: o unitate pe următoarea magnitudine mai mare (zeci) și resetare la 0 pe cifra unitară. În binar este același lucru: când ajungem la 1, care este ultimul număr unitar, adăugăm 1 la următoarea magnitudine superioară și începem din nou de la 0 în locul unitar:
Continuăm să numărăm ca de obicei: în zecimal, următorul număr după 2 este 3, în binar, după 0 avem 1:
Apoi, în zecimal, e simplu: după 3 vine 4. În binar, pentru că pe locul unităților am ajuns la 1, trebuie să pornim din nou de la 0 și să adăugăm o unitate la următoarea magnitudine superioară. Dar, deoarece deja avem 1 pe acel loc și din moment ce nu există 2 în binar, adăugăm o unitate la următoarea magnitudine superioară, corespondentul “sutelor” în zecimal, și de asemenea resetăm și echivalentul “zecimalelor” la 0:
Apoi, în zecimal, știm că urmează 5, în timp ce în binar, începem să numărăm din nou unitățile:
Din nou, în zecimal, următoarea cifră este 6, în timp ce în binar am ajuns din nou la punctul unde unitățile sunt 1, adică ultima cifră posibilă, deci trebuie să le resetăm la 0 și să adăugăm o unitate la următoarea magnitudine superioară:
Continuăm mai apoi în mod normal:
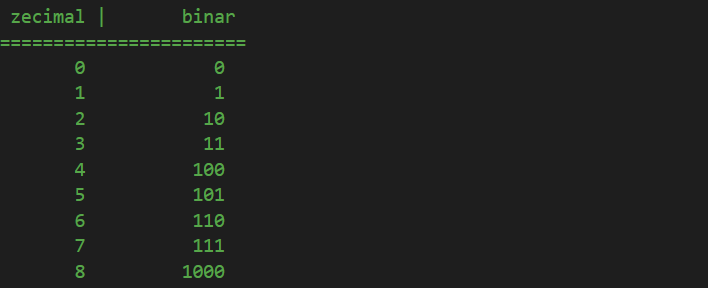
Acum, din nou, în sistemul zecimal, după 7 știm că urmează 8. În binar, am ajuns la punctul în care toate cele trei cifre sunt ultimul număr, 1, așa cum în zecimal 999 este punctul când toate cele trei cifre sunt la ultima valoare posibilă, numărul 9 și trebuie să le resetăm pe toate la 0, în timp ce adăugăm o unitate pe locul miilor. La fel procedăm și în binar:
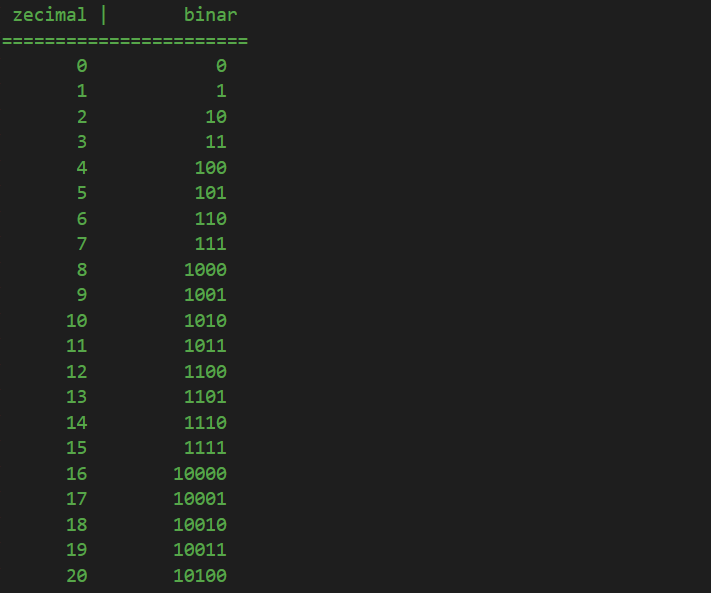
Și continuă în același mod la infinit, pe baza acelorași principii pe care le-am descris mai sus:
Evident, la un moment dat, dacă doriți să convertiți un număr zecimal mare în reprezentarea sa binară, nu veți începe să numărați de la 0. În schimb, putem folosi o formulă valabilă pentru conversia oricărui număr zecimal într-un număr binar. Tot ce trebuie să facem este să ne împărțim în mod constant numărul respectiv la 2 și să stocăm resturile acestor împărțiri. Numărul binar este reprezentat de aceste resturi, ordonate de la ultimul spre primul, astfel:

Sursă imagine
Când doriți să convertiți un număr din binar în zecimal, deplasându-vă de la dreapta la stânga, cifrele dintr-un sistem în baza 2 reprezintă puteri ale lui 2 (1, 2, 4, 8 etc. sau 2^0, 2^1, 2^2, 2^3, etc). Valoarea unui număr reprezentat ca binar este suma valorii fiecărei cifre binare înmulțită cu puterea corespunzătoare a lui 2. Exemplu:
Deci, dacă avem numărul binar 101101, putem vedea că reprezentarea sa zecimală este 45:
Conceptele explicate în această lecție sunt prezentate și vizual, ca parte a următorului videoclip:
Tags: binar, bit, numărare binară, octet