I was explaining in a previous lesson that at the deepest level, computers store and process information only as two values, 0 and 1. These values are the smallest individual pieces of information inside a computer, and they are called bits. A bit can only contain a single value at a time, either a 0 or a 1. A group of eight bits is called a byte, and sometimes, a word. A byte is the smallest piece of memory that a computer can directly manipulate. It is also equal to a single character, or letter. So, when we type the letter A, we now know that it requires 1 byte, or 8 bits, to be stored inside the memory.
The last aspect of this lesson is usually harder to grasp, specially by the beginners. However, this is not mandatory to be learned, you can still be great programmers even without knowing to directly count in binary.
If you remember from math lessons, binary counting, also known as base 2 counting, is counting using only two values, 0 and 1. According to the same principle, decimal counting, also known as base 10 counting, is counting using 10 values, from 0 to 9. So, we can say that in the decimal system, we start from 0 and the upper limit is 9, after which we need to add a new unit on a higher magnitude. Similarly, in the binary system, we start counting from 0 and the upper limit is 1, after which we also need to add a new unit on a higher magnitude. Binary counting is really the same as decimal counting, with the only difference of using only the first two numbers from it.
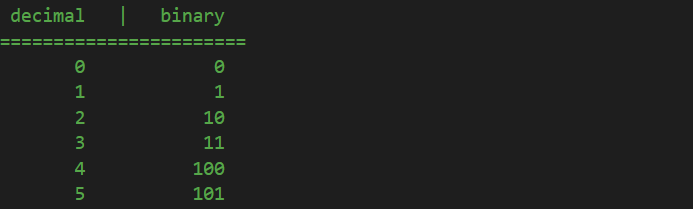
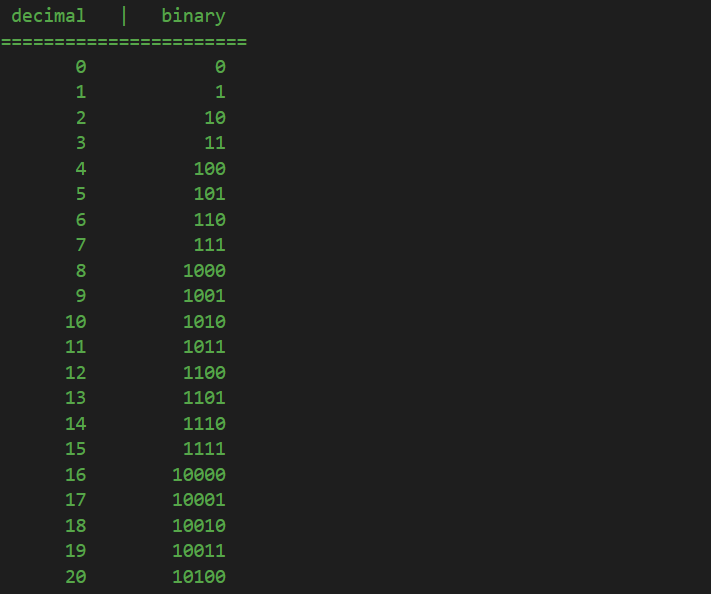
So, lets start counting in both binary and decimal system, for comparison. In both systems, we start with 0:
The next number is in both systems 1:
Here, the similarities end. In the decimal system, the number after 1 is 2. However, since there is no value 2 in binary, because the system ends at 1, we can consider that reaching 1 in binary (the last unitary number in binary) is the same as reaching 9 in decimal (the last unitary number in decimal). When we reach 9 in decimal, we add a unit on the next higher magnitude, and start counting the units from 0 again. In other words, in decimal, after 9, we have 10: a unit on the next higher magnitude (tens) and starting again from 0 on the unitary digit. In binary it is the same: when we reach 1, which is the last unitary number, we add 1 on the next higher magnitude and start again from 0 on the unitary place:
We continue counting as usual: in decimal, the next number after 2 is 3, in binary, after 0 we have 1:
Next, in decimal, its simple: after 3 it comes 4. In binary, because on the units place we reached 1, we need to start from 0 again, and add a unit on the next higher magnitude. But since we already have 1 on that place too, and since there is no 2 in binary, we add a unit on the next higher magnitude, the “hundreds” correspondent in decimal, and we also reset the “tens” equivalent to 0:
Then, in decimal, we know 5 follows, while in binary, we start counting the units again:
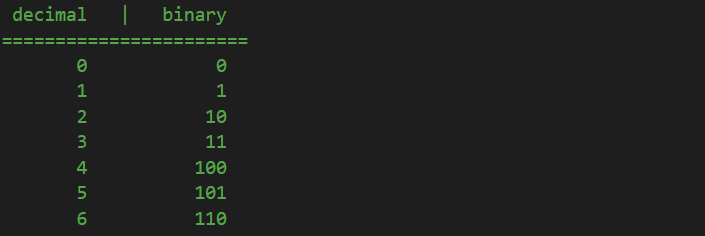
Again, in decimal, next is 6, in binary we reached again to the point where units are 1, the last digit, so we need to reset them to 0 and add a unit on the next higher magnitude:
We keep going as usual:
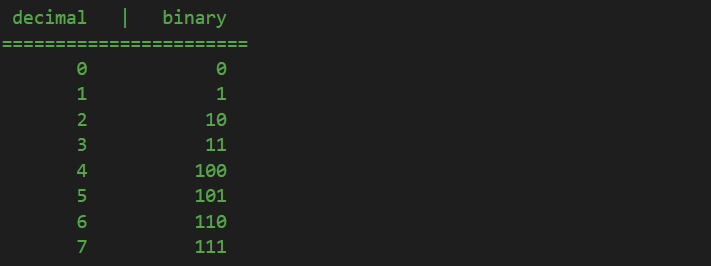
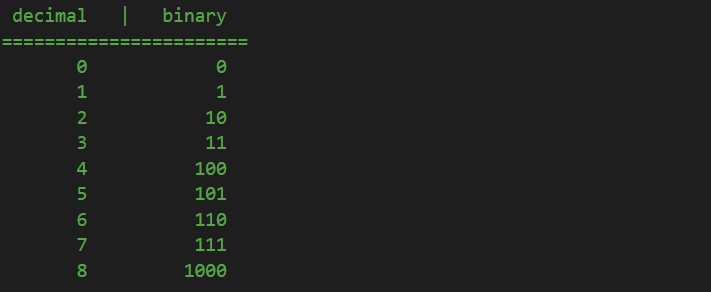
Now, again, in the decimal system, after 7 we know that it follows 8. In binary, we reached the point where all three digits are the last number, 1, as in decimal 999 is when all three digits are at the last possible number, 9, and we need to reset them all to 0 and add a unit on the thousands place. It is the same in binary:
And it goes like this forever, based on the same principles I described above:
Obviously, at some point, if you want to convert a large decimal number to its binary representation, you won’t start counting from 0. Instead, we can use a formula that is valid for converting any decimal number to a binary number. All we need to do is constantly divide our number by 2 and store the remainders of these divisions. The binary number are these remainders, ordered from the last one towards the first one, like this:

Image source
When you want to convert a number from binary to decimal, moving from right to left, the digits in a base 2 system represent powers of 2 (1, 2, 4, 8, etc. or 2^0, 2^1, 2^2, 2^3, etc). The value of a number represented as binary is the sum of the value of each digit multiplied by the appropriate power of 2. Example:
So, if we have the binary number 101101, we can see that its decimal representation is 45:
The concepts explained in this lesson are also shown visually as part of the following video:
Tags: binary, binary counting, bit, byte