Just like the binary representation, of which I have discussed in the previous lesson, hexadecimal notation is just another form of representing numbers. So, hexadecimal numbers, at their core, are normal numbers, represented in base 16, instead of base 10, as for the decimal numbers. Which means that a hexadecimal number has 16 values, starting at 0 all the way up to 9, but because we can’t count the next one as 10, which is not a single digit representation, we keep using letters, starting from A and ending with F.
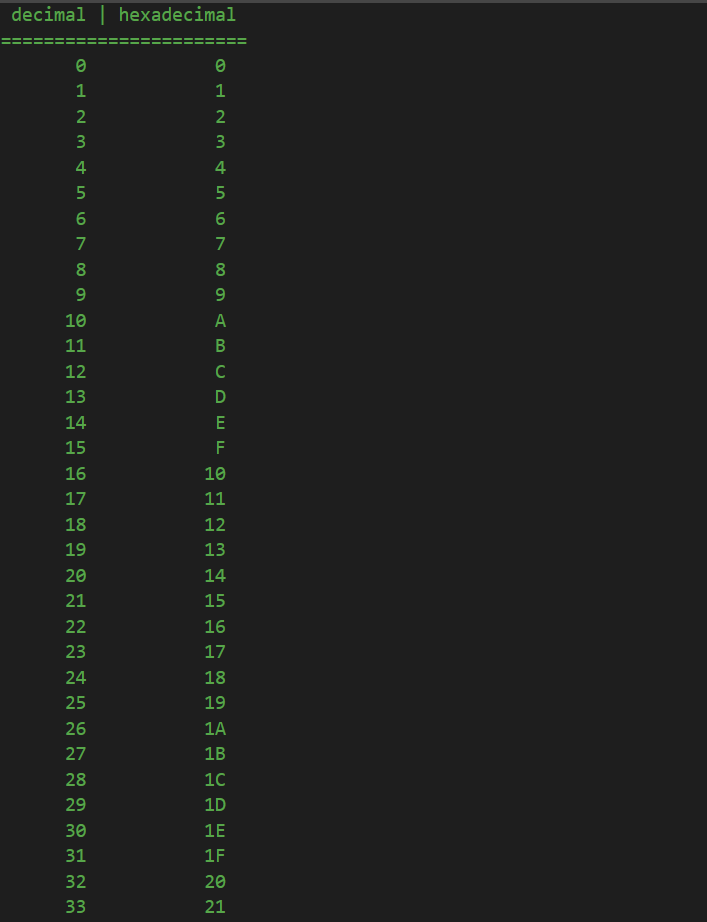
Based on the previous lesson, the same principle applies to counting in hexadecimal too:
So, whenever we reach 9 in decimal, we add a unit on the next higher magnitude (tens) and reset the unit to 0. In hexadecimal, we keep going on with letter A, B, C, D and F. Only when reaching letter F are we in the same situation as in decimal when we reach 9 and we need to add to the next higher magnitude. So, after letter F in hexadecimal, we add a unit on the next higher magnitude and reset the units to 0 again, meaning 10. But, be aware, 10 in hexadecimal is not the same thing as 10 in decimal. 10 in hexadecimal is the 17th value, starting from 0, while in decimal, its the 10th.
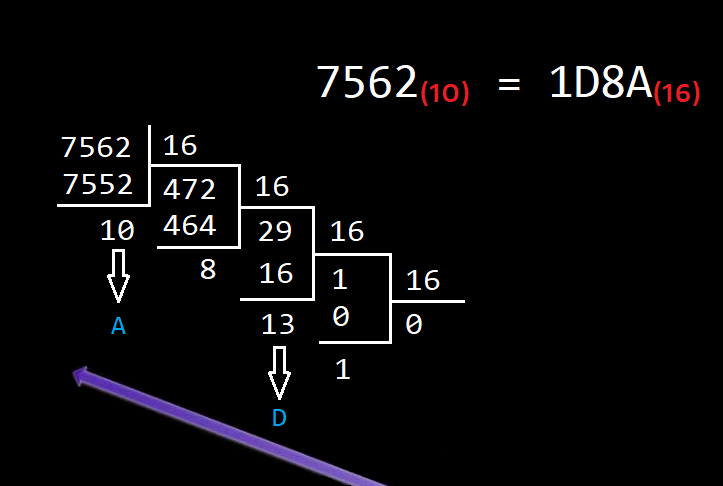
To be able to calculate any hexadecimal number, you need to constantly divide your number by 16 and take the remainders in the inverse order, from last to first, just like we did for calculating binary numbers. The only difference is the fact that whenever we have a remainder that is greater than 9, we need to remember that we are using hexadecimal values, and we can convert those two digits remainder to their hexadecimal, single digit notation:
In other words, we divide 7562 by 16 and we get 472, remainder 10. Then, we keep dividing 472 by 16, keeping the remainder, and so on, and so forth. At the end, when we can no longer divide by 16, we take the remainders in the opposite order, from end to finish, and whenever we encounter remainders that are greater than 9, we convert them to the hexadecimal notation (13 in decimal is D in hexadecimal, 10 in decimal is A in hexadecimal, etc).
To calculate a decimal number from a hexadecimal one, we need to remember that each hexadecimal digit represents a value to be multiplied by a power of 16. Example:
Therefore, we can calculate the decimal representation of a hexadecimal number, such as 1A2F, like this:
In C#, and many other languages, hexadecimal values are prefixed with a 0x part, so that people can understand that it is a hexadecimal value and not a decimal one. That means that hexadecimal 1A2F will be represented in C# as 0x1A2F.
Tags: bit, byte, hexadecimal, hexadecimal counting