Follow the white rabbit

In some cases, you will see programmers that represent decimal or binary values using hexadecimal values. Why is that?

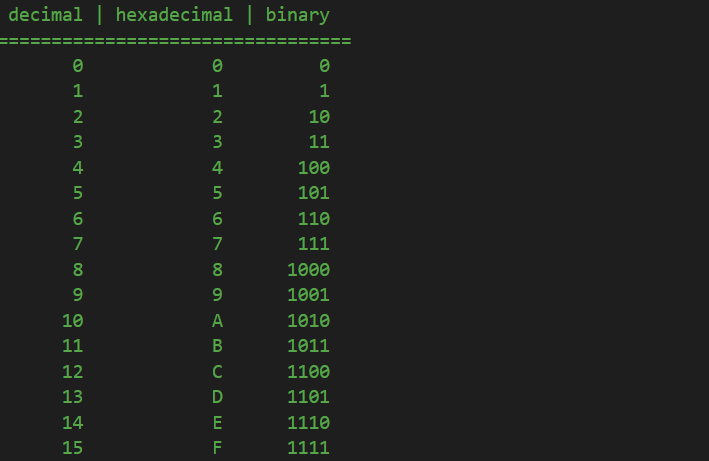
Well, since we now know from previous lessons how to count in both binary and hexadecimal, let’s see how a few of these numbers correspond:

If you look closely to the above relationship, you will quickly notice that the maximum value a hexadecimal digit can store is equal to exactly the maximum number 4 bits can store. In other words, one hexadecimal digit can exactly represent 4 binary digits. Now, consider we want to see how a number is stored as a binary value in RAM. Lets take the number 2,047,483,647:

You can already start to see that visualizing it as binary values is extremely hard: 31 bits of data and one bit for the sign. On the other hand, since one hexadecimal digit can represent 4 bits, that means that we can represent a byte (8 bits) using only 2 hexadecimal digits, instead of 8 separate bits. For this reason, all those 32 bits representing 0111 1010 0000 1010 0001 1110 1111 1111 in binary are now much more easier to read and comprehend when we see them as a hexadecimal value representing 7A0A1EFF. And it is only logical: 8 hexadecimal digits multiplied by 4 binary digits per hexadecimal digit are equal to 32 binary digits, which is exactly the number of bits an int needs to be stored in RAM.

Arguably, we could try and represent those 31 bits with decimal values, except 10 (the number of values per each decimal digit) does not divide with any power of 2, neither 4 nor 8. Which means we can’t use a decimal digit to represent a byte (8 bits) or half of it (4 bits). On the other hand, since hexadecimal digits can store 16 values, from 0 to F, they can be used to store 2 bytes per each digit, because 16 can be divided by 8, which is the number of bits a byte has.

So, as a summary, the reason why some programmers use hexadecimal values for their integer values is that they are actually using a convenient way of seeing exactly the bits stored in memory for that integer. And, you have to agree, for 32+ bit integers the risk of mistake with 4294967295 is much higher than 0xFFFFFFFF.

When we will discuss enumeration flags and bit masks, we will get to see how much easier is to manipulate individual bits inside a larger data type using hexadecimal values.

Tags: binary, hexadecimal

This entry was posted on Monday, December 26th, 2016 at 08:44 and is filed under Introduction. You can follow any responses to this entry through the RSS 2.0 feed. You can skip to the end and leave a response. Pinging is currently not allowed.