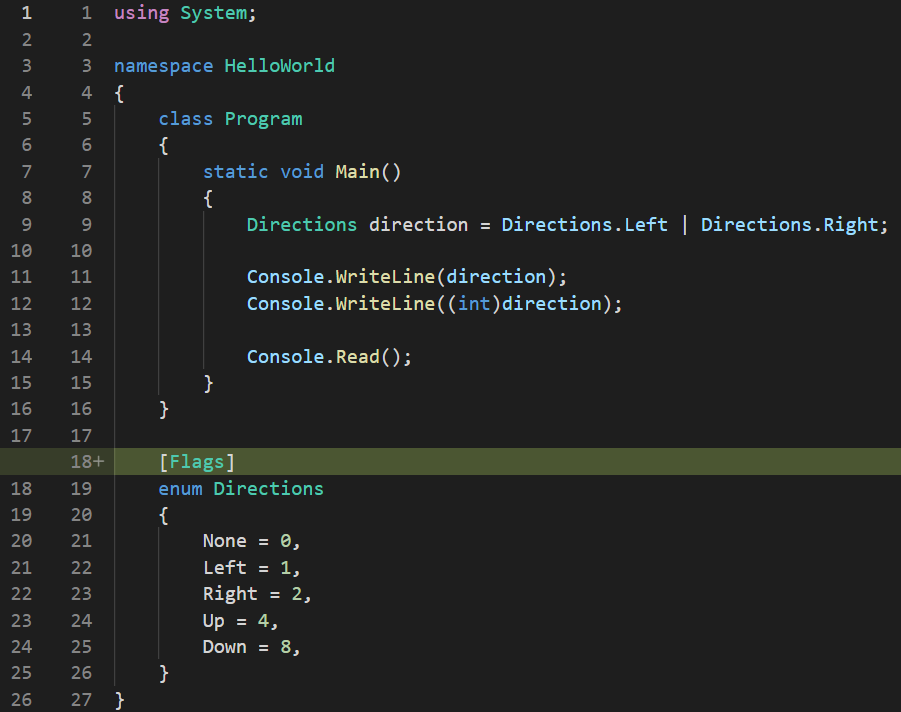
Most programmers use enums just so they can enforce a predefined set of options from which users can chose. However, enums have one major disadvantage: they can only hold one value at a time. Let’s say we have the following code:
[raw][/raw]
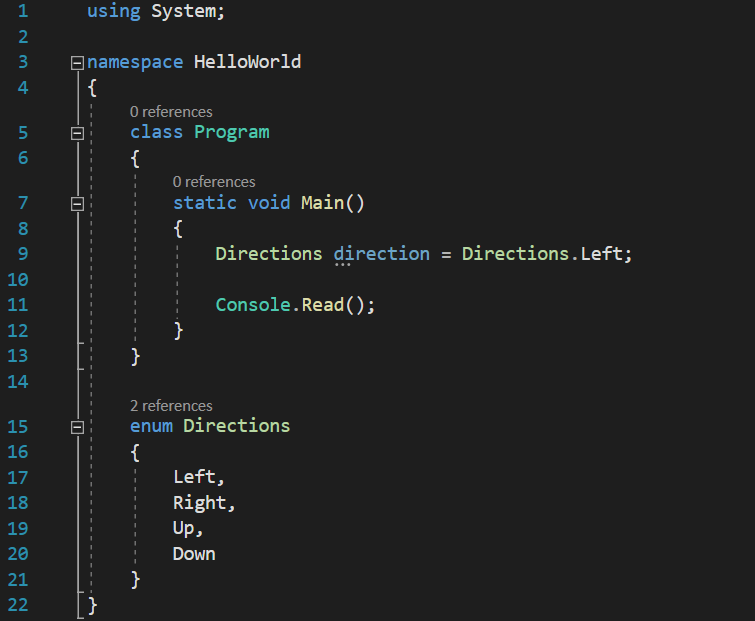
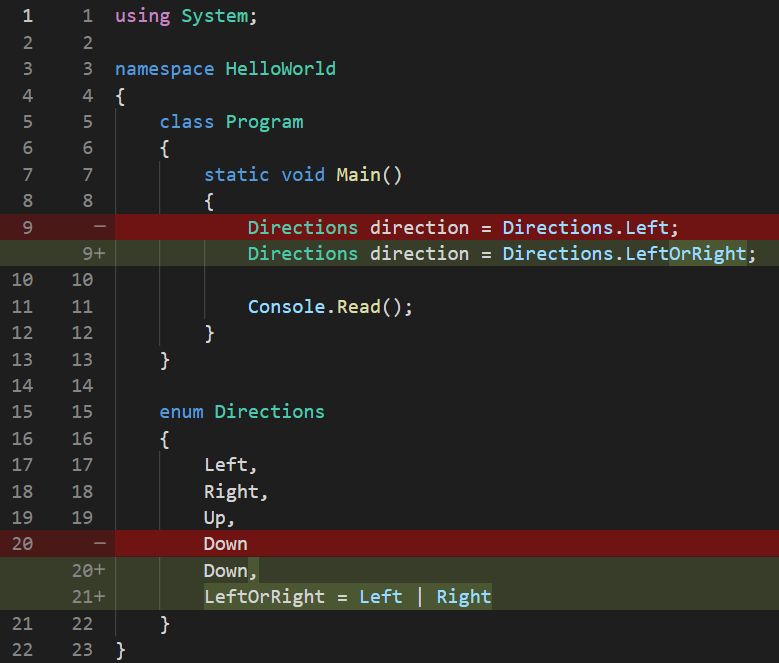
In this case, specifying that we want to have a direction towards left seems OK. But, what if we want to specify two directions at once? Let’s assume we have the code for a unit inside a game, and we want to specify that it can move left or right. How can we do that, since the directions enum can only hold one value at a time, either Directions.Left or Directions.Right?
To solve this, we can actually use some clever programming bit operations on two or more values, process named masking, because it basically means the same thing as to when we cut holes in a paper so that spray paint only paints through the parts that we want. In this case, the cut paper becomes a mask, allowing paint only through the punched holes. Similarly, we could use binary operators to “let through” or “not let through” two or more values of an enum, assigned to a single variable. For instance:
See code changes
Legend:
[/raw]
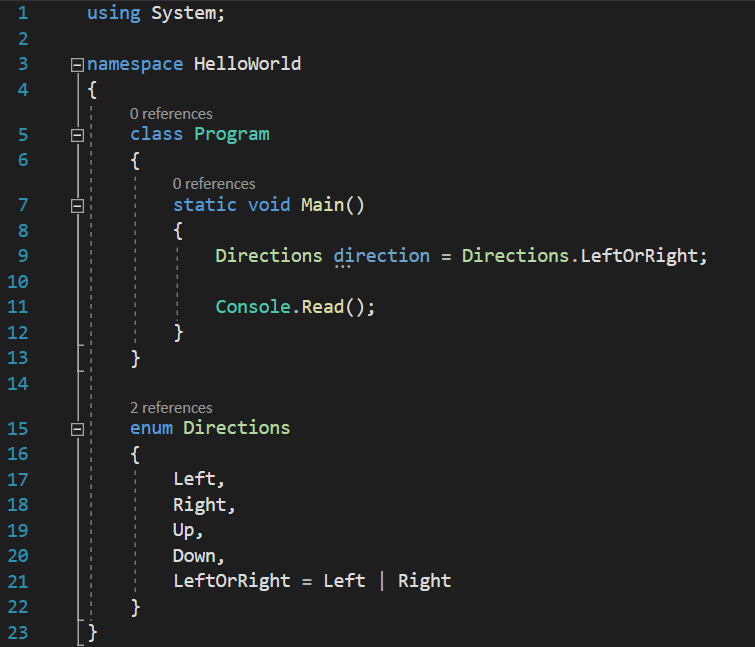
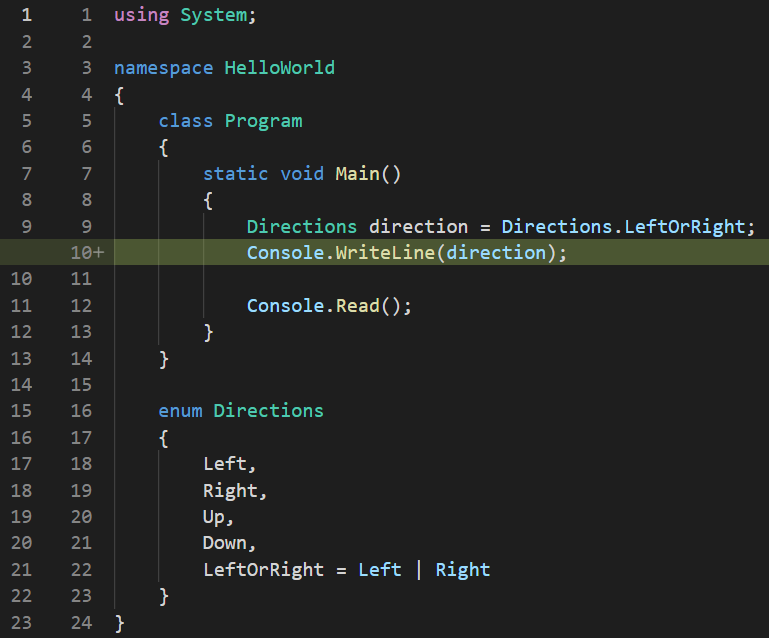
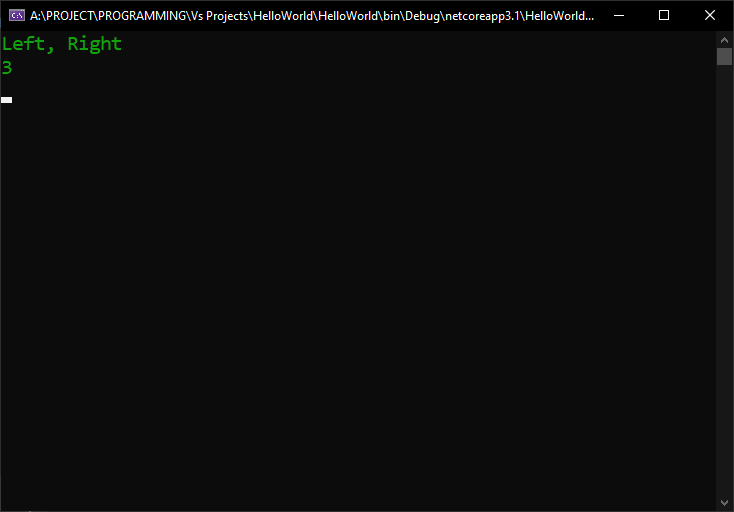
You would think that this solved our problem, since now Directions.LeftOrRight value stores both a Directions.Left and a Directions.Right inside it, but… does it? Let’s check by displaying the value to the console:
See code changes
Legend:
[/raw]

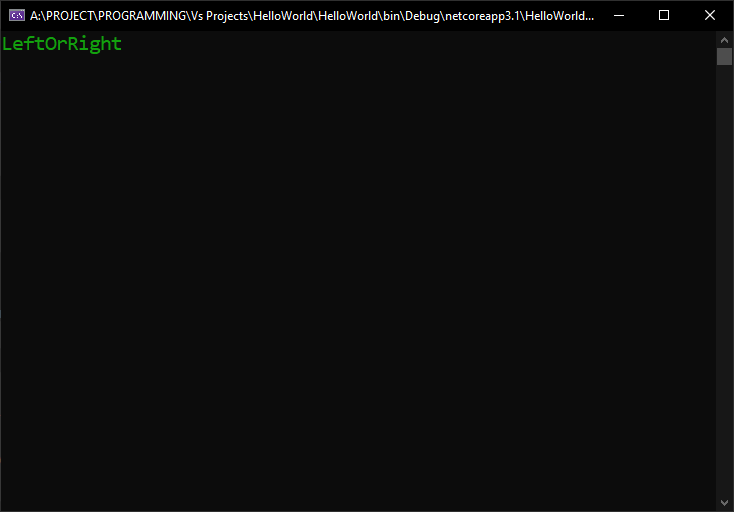
We will see that the output would be this:
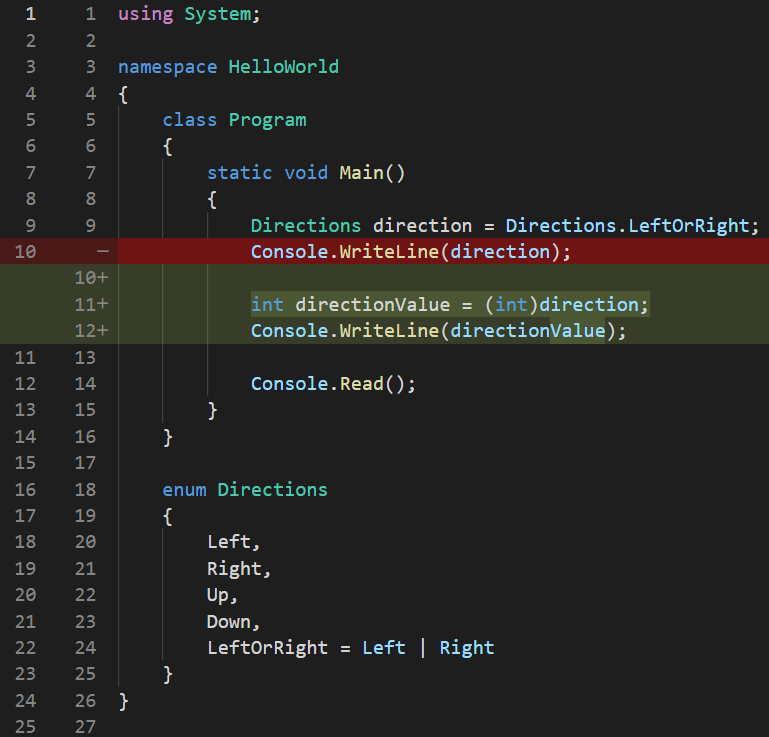
So far, so good, it does seem to be the value that we assigned to it. But, how about the integer value that is stored internally? Remember, any enumeration element is actually just a nice name given to an integer value, as we learned in the previous lesson. So, let’s see this value, by casting the enumeration value to an int and printing it at the console:
See code changes
Legend:
[/raw]
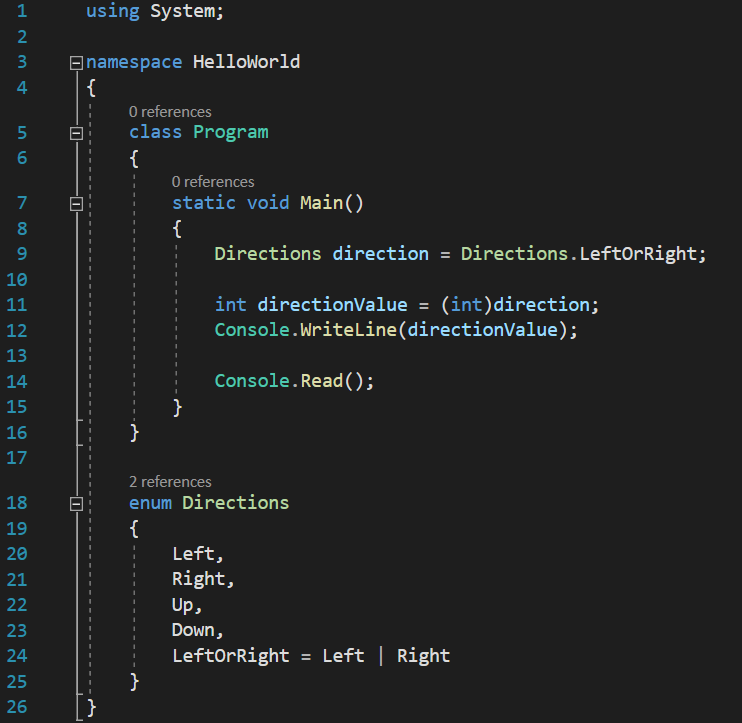
And now the console reads:
Oh-oh! Not good news, it seems. Remember how I said in the enumerations lesson that if we do not manually specify integer values to the elements of the enumeration, the compiler will automatically assign each of them a numeric consecutive and ascending value, starting from 0? Well, considering we haven’t given any integer values to our enumeration’s elements, the above value of 1 displayed on the console would mean the second value automatically assigned by the compiler to the elements of the enumeration, in other words, the number assigned by the compiler to the Directions.Right element. Can this be true? Could Directions.Right and Directions.LeftOrRight have the same value? Let’s check!
See code changes
Legend:
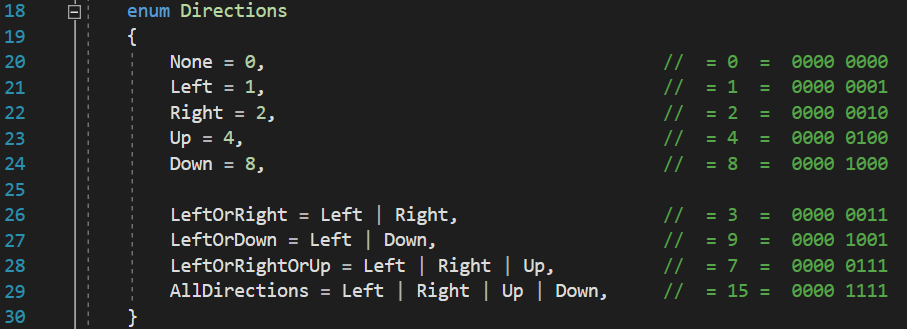
[/raw]
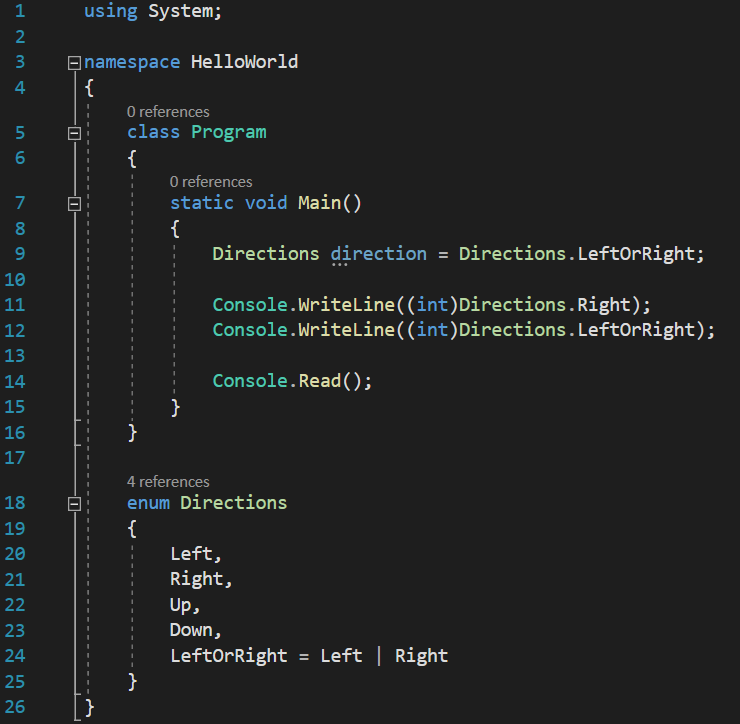
And here is the output:
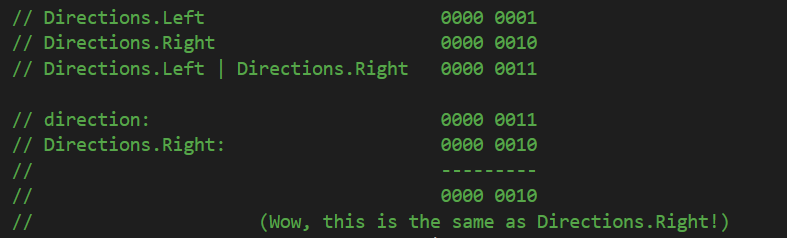
So, yes, two different enum elements hold the same value, which is very bad for us, since we can’t tell which one we actually use in our codes. So, first of all, why does this happen? To answer this question, let’s see how these numbers are actually binary represented in RAM:
You only have to remember from the lesson bitwise operators that when we are performing a binary OR operation between two bits, the resulting binary value is 1 if at least one of the operands have a value of 1, and 0 only when all the operands have a value of 0. In our case, because we assigned no numeric values to the elements of the enum, the compiler automatically assigned 0 for Directions.Left and 1 for Directions.Right. In the image above, we can see how these two integers are represented in binary inside the RAM, and performing a binary OR operation on those two binary values will still result in a value of 1, because 0 | 1 = 1.
So, it seems that combining two bits through a binary operation is not the answer we’re looking for, because trying to combine one element with a value of zero with an element containing a value of 1 results in the resulting value still having a value of 1, when we were actually hoping for a whole different value, so we can differentiate between Directions.Left, Directions.Right and Directions.LeftOrRight.
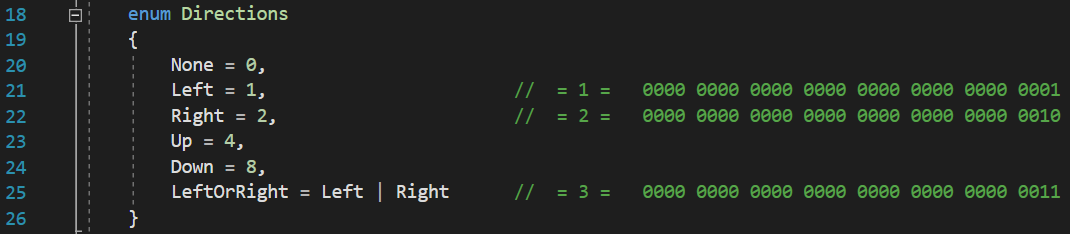
One might wonder, “well, why not manually assign significant values to the elements of the enumeration, and start with 1, or add a new enumeration element, such as Directions.None?”, like this:
Apparently, that doesn’t seem to be working either. Assigning a value of 1 to Directions.Left and a value of 2 to Directions.Right resulted in Directions.LeftOrRight having a value of 3, after the binary OR operation. We can clearly see that a value of 3 is assigned to Directions.Up, so, no, this is no good either.
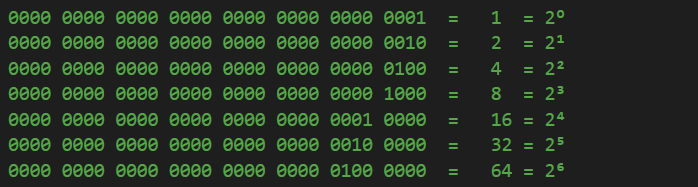
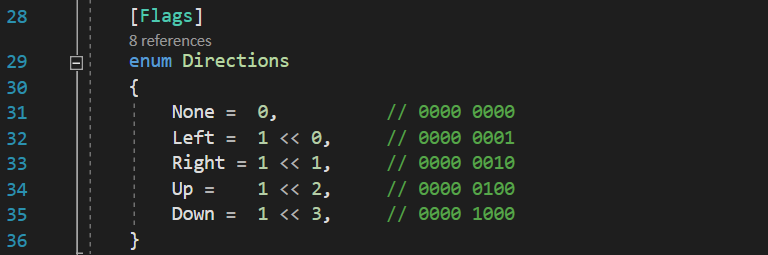
What the correct solution to our problem would be is if we were actually storing all the elements of our enumeration in such a way that each of them would have a single bit with a value of 1, on a unique different position from the rest of the elements. Something like this:
Now, each of these four binary values are different, because each of them has a single bit with a value of 1, each of them on a different position. If we try to use the OR binary operation on any two of them right now, everything would work flawlessly:
We can conclude from the above examples that since each element of the enumeration has a single bit value of 1 and it is on a different place for each of the elements, we would never conflict these bits. This is precisely what I was picturing earlier, with the paper having some holes and being used as a mask for the spray paint. In our case, having two operands with 4 bits each, we can say that the OR binary operation acts like a mask too: for a bit value of 1 to get into the operation’s result on a certain position, it requires at least one of the operand’s bits on that position to be 1, just like a hole in the paper. No hole at a certain place in the paper, no paint passes. No bit with a value of 1 in a certain position in at least one of the operands, no binary value of 1 for that position passes either.
From the above mental exercise we summarize the fact that we need to store the elements of our enumeration in such a way that their binary representation ensures a single bit with a value of 1 and that each element’s bit with a value of 1 is on a different and unique position compared to all the other elements. This is actually simpler if we take a look at a few of these numbers and their decimal representation:
Somehow, advancing the position of the bit with a value of 1 by one place towards the left for each of the values results in a decimal value that is a consecutive power of 2. Which means that those are the values we have to give to our enumeration:
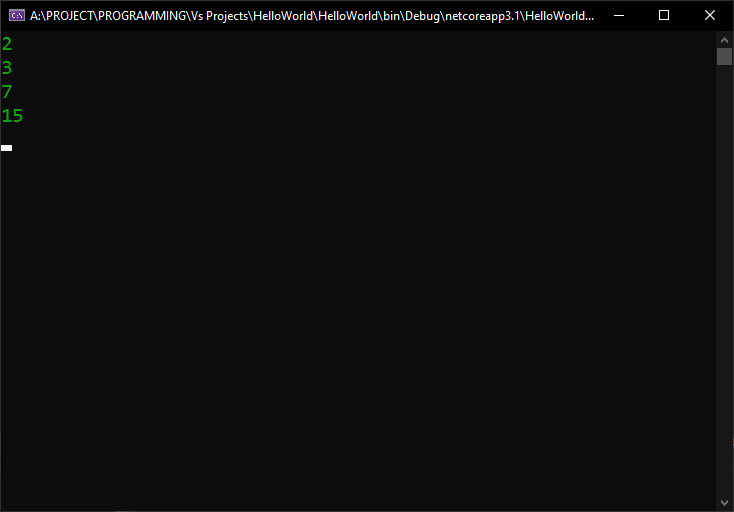
Now, we still have a value of 1 for Directions.Left, 2 for Directions.Right and 3 for Directions.LeftOrRight. The only difference, compared to the previous code is that the value of 3 is not assigned to any of the elements of the enum. And we can test for a few more cases, even involving combinations of more than 2 operands, and we will still get the same result: none of the resulting values will be equal to the value of any of the existing elements, so, we will not have conflicts or confusion about what elements are being used:
Mind you, we could even use the hex representation of the values, so we don’t play with 32 bits for each number, but instead see them as pairs of 2 bytes for each hexadecimal digit, as explained in the lesson hexadecimal numbers, so we end up using only 8 hexadecimal digits instead of 32 binary digits:
Much easier to see, manage and understand. Lets try and print some of the combined elements, to see how they actually appear:
[raw][/raw]
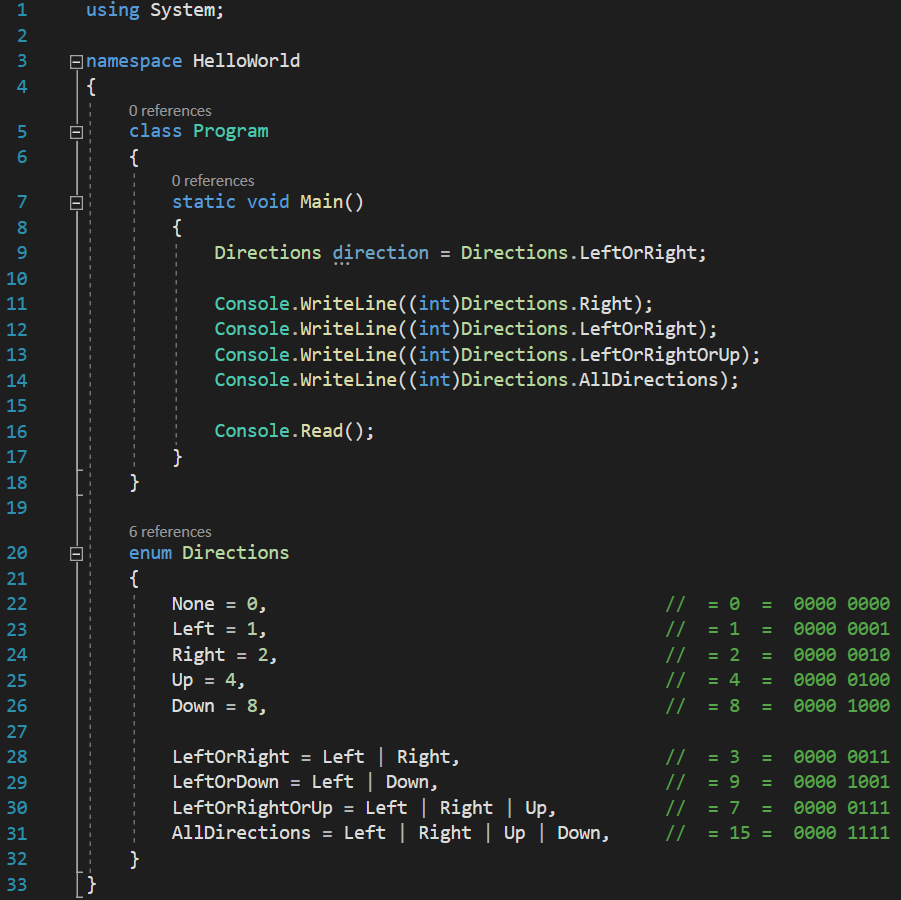
With this result:
The same values we predicted. However, it would be really, really nice to be able to see the names of the enumeration’s elements representing these values, rather than seeing the values themselves. You have to admit, Directions.LeftOrRightOrUp is much easier to remember what it means, compared to 7. Let’s see how they look by printing them directly to the console, without converting the value to an int:
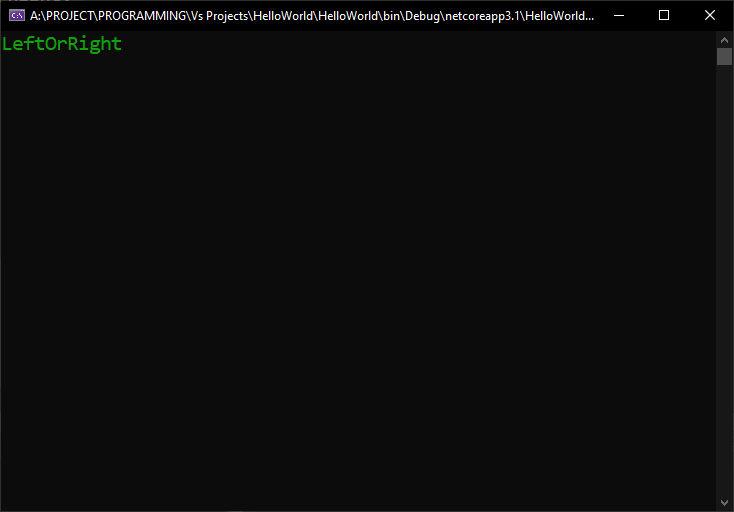
[raw][/raw]
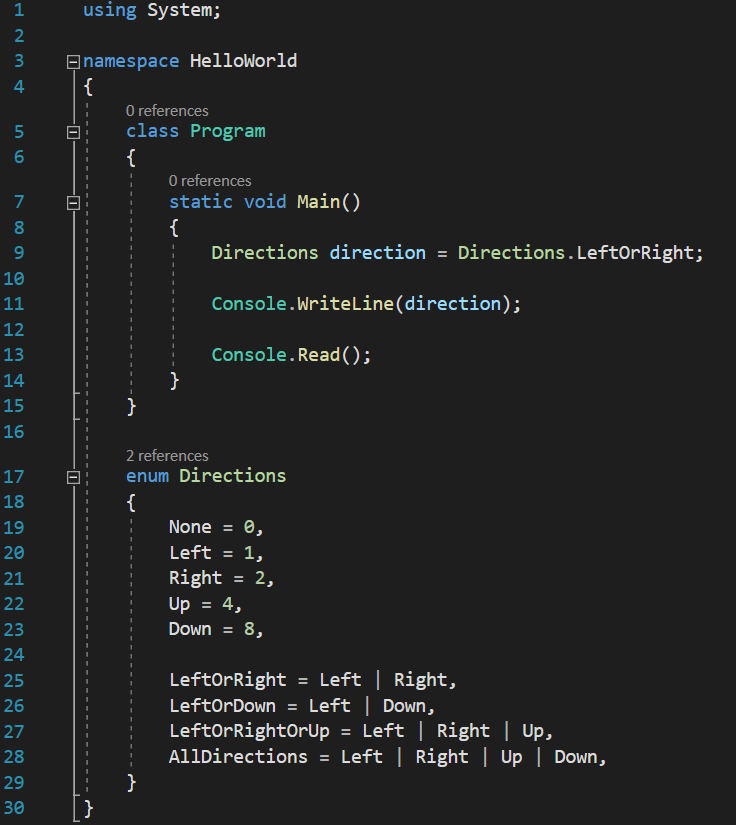
This would be the output:
Which is really nice, we do get to see a meaningful name, instead of a numeric value.
However, what if you don’t want to pollute your enumeration with combined values, such as Directions.LeftOrRightOrUp or Directions.LeftOrRight? Does it still work? Can we still combine them wherever we need a combination? Let’s try:
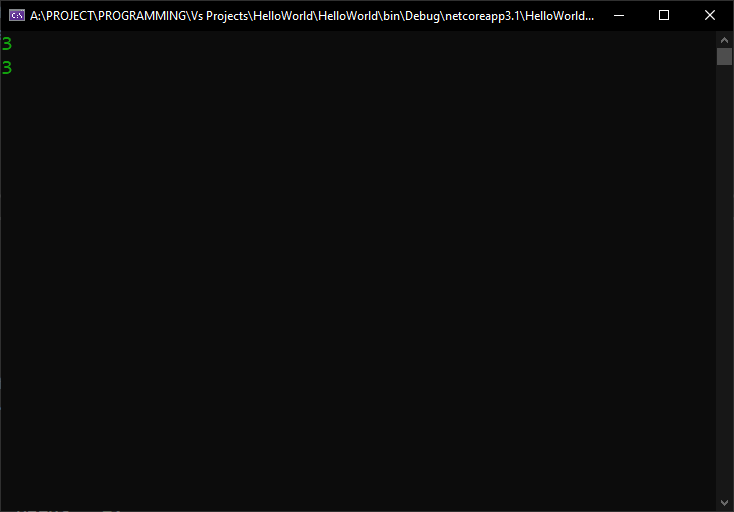
[raw][/raw]
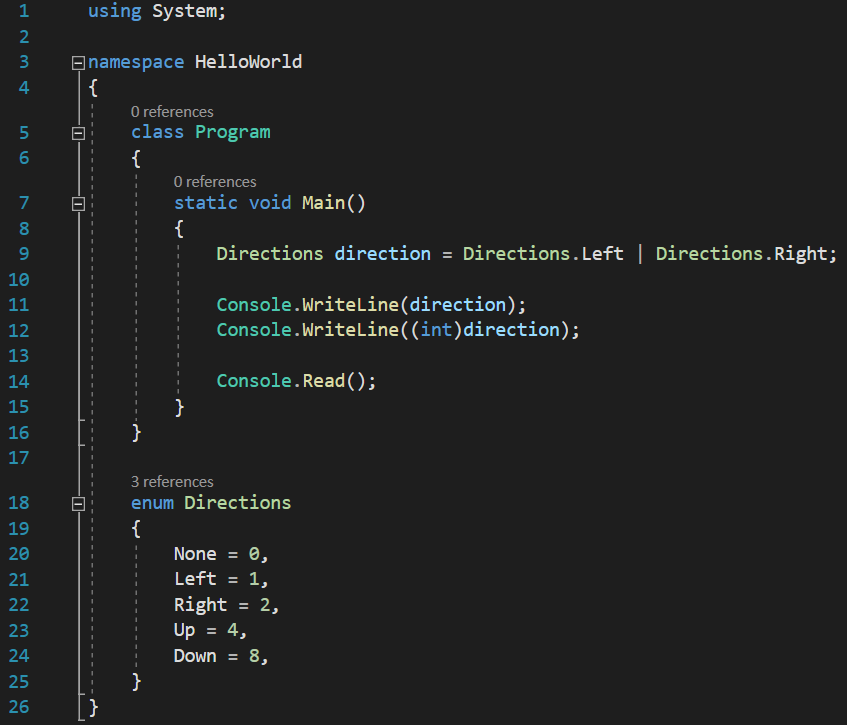
And here, the result of displaying the value both directly and converted to an int:
Sadly, as soon as we deleted the combined elements from our enumeration, the result of displaying a combination of two elements of the enumeration will still be only a numerical value, even without converting it to an int. So, do we have a solution for not hardcoding these combinations in our enumerations, and still get the nice naming when printing them to the console?
Yes, we do! To solve this issue, enums can be decorated with an attribute called Flags, like this:
See code changes
Legend:
[/raw]

Now, if we run the program again, we get to see that even if our enumeration no longer contains combined elements inside it, if and when we chose to combine such elements, they are displayed much nicer at the console:
That means that by simply placing the Flags attribute on the enumeration, we instructed the compiler to actually treat the elements of our enumeration as bit masks, and to acknowledge that we can have combinations of such masks/elements.
So, keep in mind, the Flags attribute does NOT enable us to use bit masks, as most programmers incorrectly believe, it is actually just telling the compiler itself that we want the elements of that enumeration to be treated as a bit masks, so it displays possible combinations of them in a nicer and more intelligible form. But, if we don’t care about how they are displayed, as long as the enumeration’s elements are assigned values using powers of 2, bit masking works just as perfectly, even without the Flags attribute. It is recommended to use it though, even if just to signal to other programmers the intentioned usage of the enumeration.
Another thing to keep in mind is that only specifying the Flags attribute on an enum does NOT automatically assign power of 2 values to the elements of that enumeration. If you don’t manually specify those values, or if you don’t specify them correctly as unique powers of 2, the bit masking will still fail, even when using the Flags attribute.
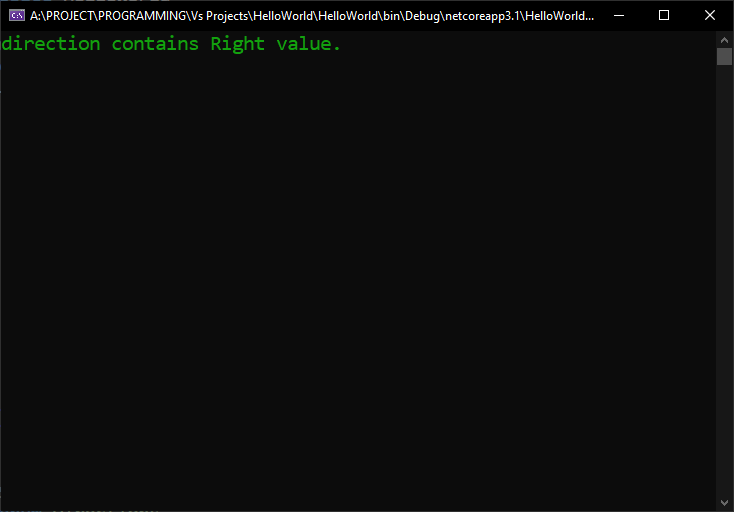
If you want to check if the value of a combined enumeration element contains a certain element inside it, you can use the enumeration’s HasFlag() function, like this:
[raw][/raw]
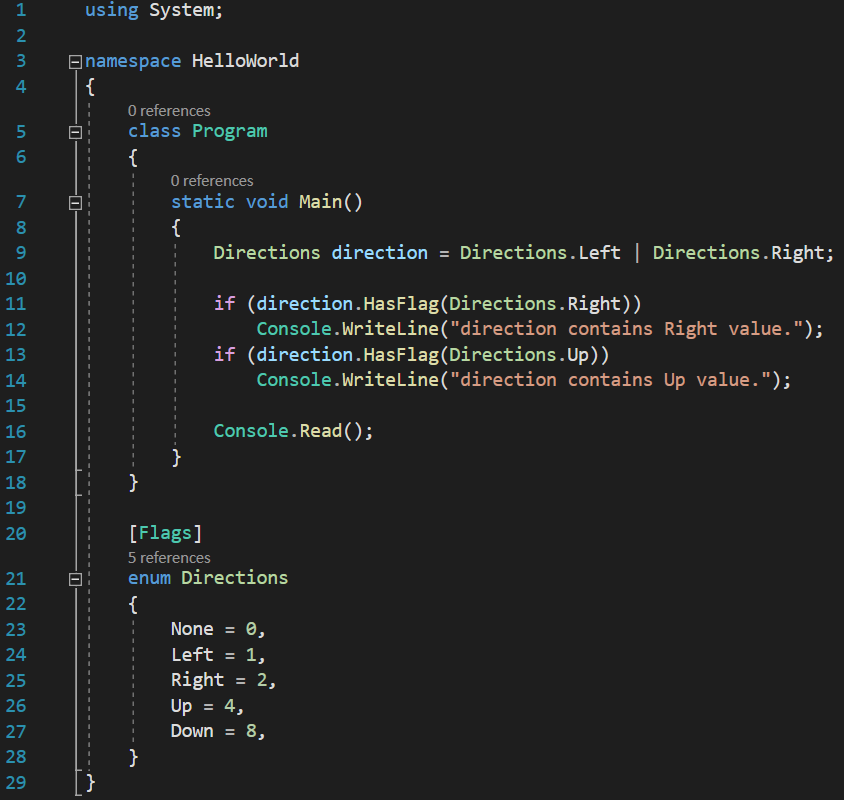
And this is what the console prints:
Which is consistent with our intentions: the directions variable does contain a Directions.Right, but it does not contain a Directions.Up.
Prior to version 4.0 of the .NET framework, where the HasFlag() function does not exist, we could do the same check like this:
[raw][/raw]
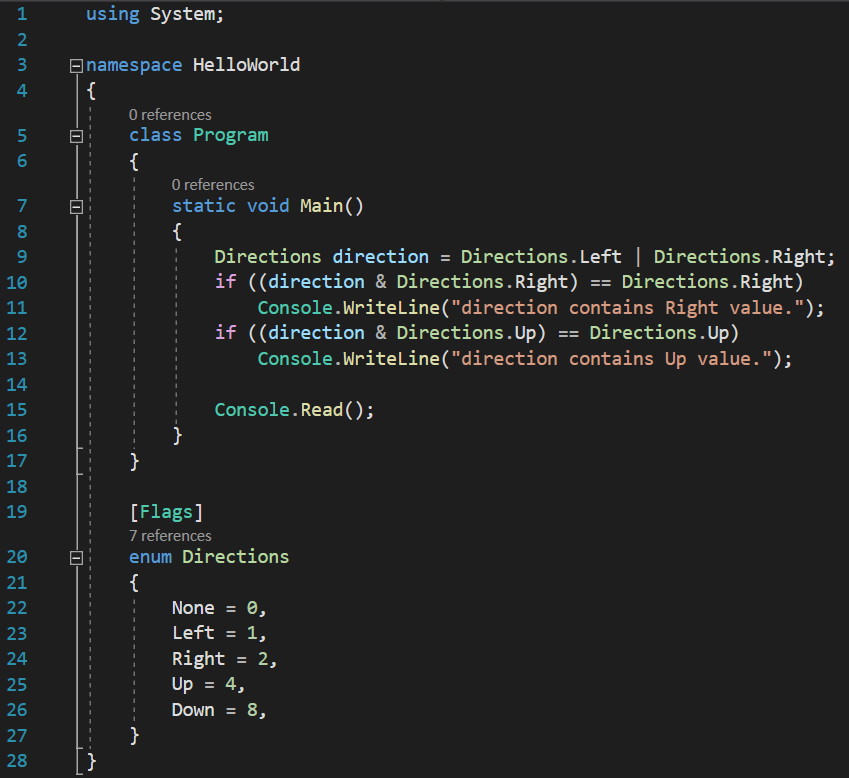
And the result would be the same. The explanation is simple: we perform a bitwise AND operation, and, as we already know, this operation only returns a value of 1 when all its operands are 1, and 0 if at least one of the operands has a value of 0.
We only have to look at the hex representation of Directions.Left, Directions.Right and Directions.LeftOrRight:
Now, with these values, we are performing a bitwise AND operation between the value of the direction variable (which is a combination of Directions.Left and Directions.Right) and the value of Directions.Right, and compare the result with the hex representation of Directions.Right:
The comparison will only be True when all the AND bitwise operation will produce the same bits as Directions.Right. And, yes, we can see that an AND operation between direction variable and Directions.Right does indeed result in the same bits as Directions.Right, and the if comparison returns a True value.
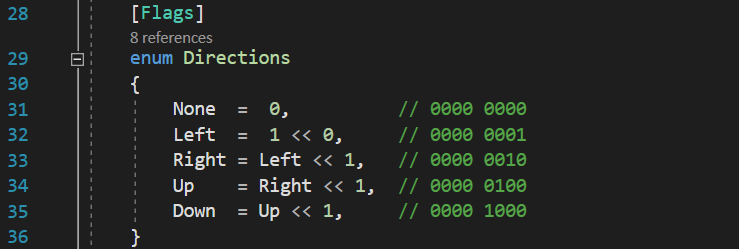
You should also know that there is another way of declaring bit mask enumerations, using bitshifting operators. Instead of manually assigning consecutive and ascending power of 2 values to the elements, we can assign to all of them a value of 1, which we then left bitshift by one additional place for each of the values:
And the resulting enumeration would be identical to the one we used before. The explanation is simple: we assign a value of 1 to all of them, because the integer 1 is represented in binary as a single bit with a value of 1, on the last position of the 32 bits. From there, we just left bit shift this bit by one additional place for each of the values, effectively “moving” it on the next places towards left.
Of course, we can also left bit shift each new value using the previous one and bit shifting by a single place each time, instead of ascending values:
The same technique of combining multiple individual values inside a single variable can be used in places where performance is of importance. For instance, if you want to create a game map of size 1,000 rows by 1,000 columns, that means 1,000,000 cells. If each of these cells uses few variables to hold information like terrain type, whether the cell is occupied by a building or not, if the units can pass it or not, etc, you can imagine that one million cells multiplied by how many variables each cell uses does no good to your RAM memory. Instead, using bit masks, it is easy to hold all these information in a single variable per cell, in which each bit of the variable represents a different value or combination of values.
Tags: binary, bit, bit mask, bit shifting, bitwise operators, flags, hexadecimal