Majoritatea programatorilor folosesc enumerările doar pentru a putea aplica un set predefinit de opțiuni din care utilizatorii pot alege. Cu toate acestea, enumerările au un dezavantaj major: pot deține o singură valoare la un moment dat. Să presupunem că avem următorul cod:
[raw][/raw]

În acest caz, specificarea faptului că dorim să avem o direcție spre stânga pare OK. Dar, dacă vrem să specificăm două direcții simultan? Să presupunem că avem codul pentru o unitate dintr-un joc și vrem să specificăm că se poate deplasa la stânga sau la dreapta. Cum putem face acest lucru, de vreme ce variabila directie poate stoca o singură valoare la un moment dat, fie Directii.Stanga sau Directii.Dreapta?
Pentru a rezolva acest lucru, putem folosi niște artificii de programare inteligente, ce implică operații pe biți pe două sau mai multe valori, proces numit mascare (masking), pentru că se referă practic la același lucru ca atunci când tăiem găuri într-o hârtie, astfel încât vopseaua dintr-un spray să vopsească doar prin părțile dorite. În acest caz, hârtia tăiată devine o mască, permițând trecerea vopselei doar prin găurile perforate. În mod similar, am putea folosi operatori binari pentru „a lăsa” sau „a nu lăsa” să treacă două sau mai multe valori ale unei enumerări, atribuite unei singure variabile. De exemplu:
Vizualizează schimbări cod
Legendă:
[/raw]
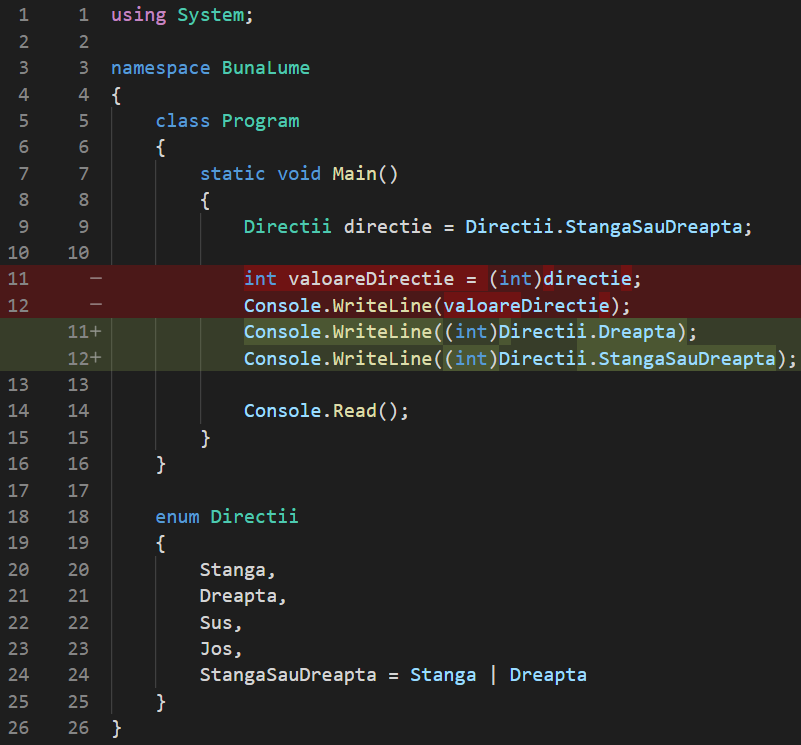
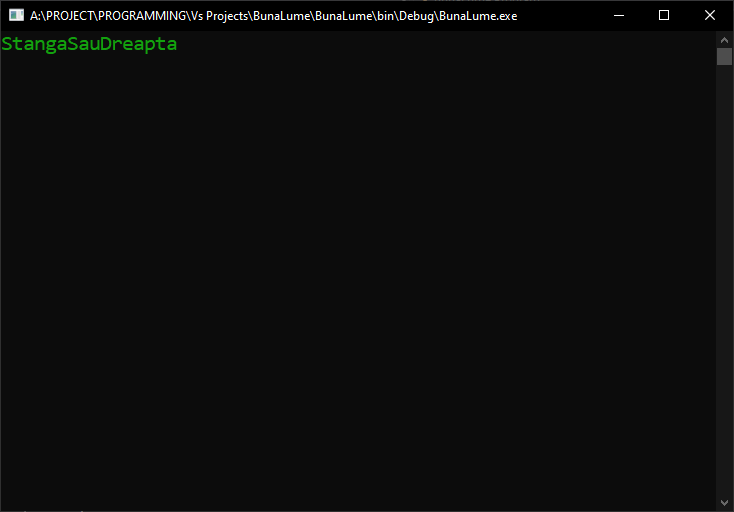
Ați crede că acest lucru a rezolvat problema noastră, deoarece acum valoarea Directii.StangaSauDreapta stochează atât Directii.Stanga cât și Directii.Dreapta în interiorul ei, dar… o face? Să verificăm, afișând valoarea la consolă:
Vizualizează schimbări cod
Legendă:
[/raw]
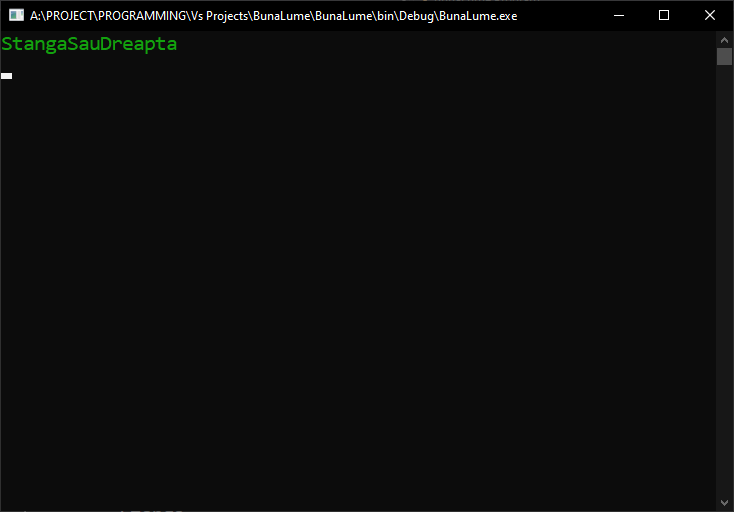
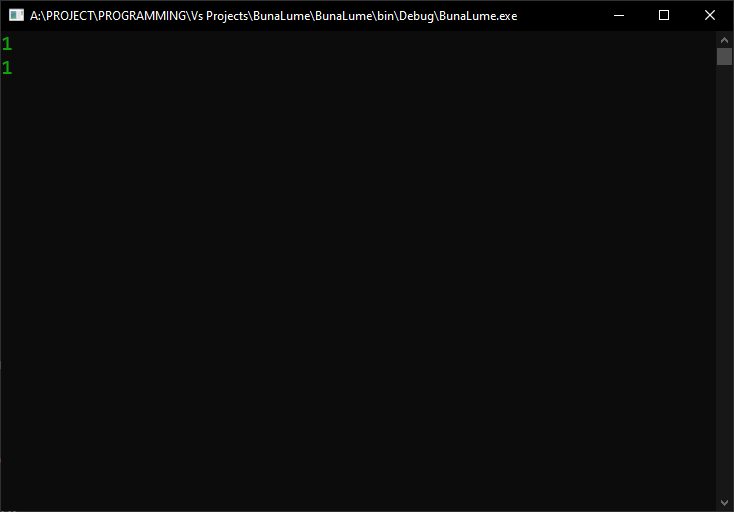
Vom vedea că rezultatul ar fi acesta:
Până acum, totul e bine, pare a fi valoarea pe care i-am atribuit-o. Dar, care e valoarea întregului care este stocat intern? Amintiți-vă, orice element de enumerare este de fapt doar un nume frumos dat unei valori întregi, așa cum am învățat în lecția anterioară. Deci, să vedem această valoare, convertind valoarea de enumerare într-un int și afișând-o pe consolă:
Vizualizează schimbări cod
Legendă:
[/raw]
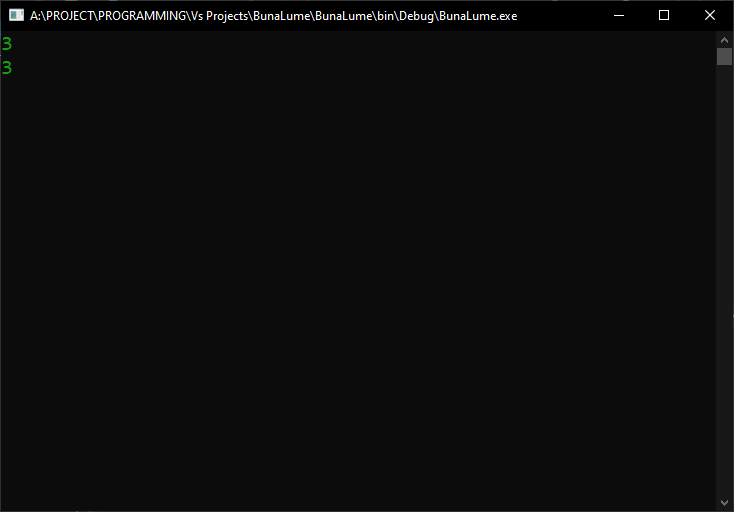
Iar acum, consola afișează:
Oh-oh! Vești proaste, se pare. Vă amintiți cum am spus în lecția despre enumerări că dacă nu specificăm manual valori întregi elementelor enumerării, compilatorul va atribui automat fiecăreia dintre ele o valoare numerică consecutivă și crescătoare, începând de la 0? Ei bine, având în vedere că nu am dat nici o valoare întreagă elementelor enumerării noastre, valoarea 1 de mai sus afișată pe consolă ar însemna și a doua valoare atribuită automat de compilator elementelor enumerării, cu alte cuvinte, numărul atribuit de compilator elementului Directii.Dreapta. Poate fi adevărat? Ar putea Directii.Dreapta și Directii.StangaSauDreapta să aibă aceeași valoare? Să verificăm!
Vizualizează schimbări cod
Legendă:
[/raw]
 Iar acesta este rezultatul:
Iar acesta este rezultatul:
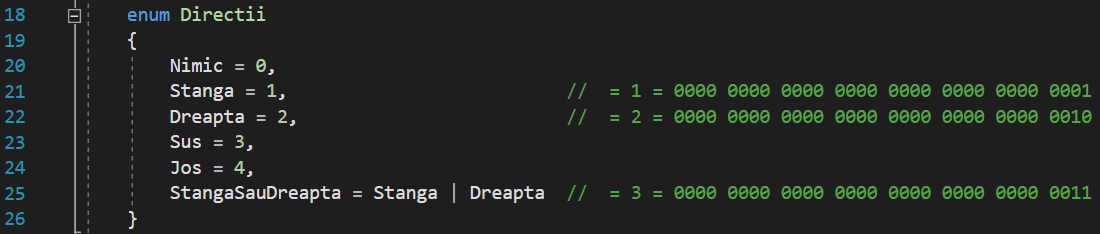
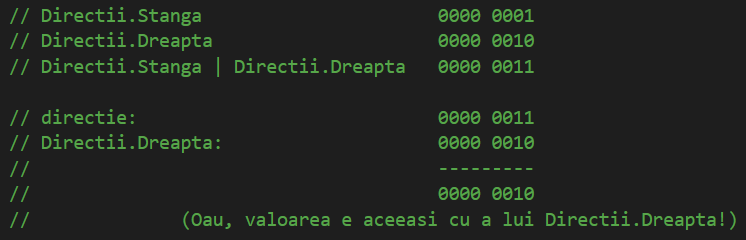
Deci, da, două elemente enum diferite dețin aceeași valoare, ceea ce este foarte de nedorit pentru noi, deoarece nu putem spune pe care din ele o folosim de fapt în codurile noastre. Deci, în primul rând, de ce se întâmplă acest lucru? Pentru a răspunde la această întrebare, să vedem cum sunt reprezentate binar în memoria RAM aceste numere:
Trebuie doar să vă amintiți din lecția despre operatorii pe biți că atunci când efectuăm o operație binară SAU între doi biți, valoarea binară rezultată este 1 dacă cel puțin unul dintre operanzi are o valoare de 1 și 0 numai atunci când toți operanzii au valoarea 0 . În cazul nostru, deoarece nu am atribuit valori numerice elementelor enumerării, compilatorul a atribuit automat 0 pentru Directii.Stanga și 1 pentru Directii.Dreapta. În imaginea de mai sus, putem vedea cum aceste două numere întregi sunt reprezentate binar în interiorul memoriei RAM și cum efectuarea unei operații SAU binare pe aceste două valori va duce în continuare la o valoare de 1, deoarece 0 | 1 = 1.
Deci, aparent, combinarea a doi biți printr-o operație binară nu este răspunsul pe care îl căutăm, deoarece încercarea de a combina un element cu o valoare zero cu un element care conține o valoare de 1 are ca rezultat valoarea o valoare tot de 1, pe când noi speram de fapt o valoare complet diferită, astfel încât să putem face diferența între Directii.Stanga, Directii.Dreapta și Directii.StangaSauDreapta.
V-ați putea întreba: „păi, de ce să nu atribuim manual valori semnificative elementelor enumerării și să începem cu 1, sau să adăugăm un nou element de enumerare, cum ar fi Directii.Nimic?”, astfel:
Aparent, nici această idee nu pare să funcționeze. Atribuirea unei valori de 1 la Directii.Stanga și o valoare de 2 la Directii.Dreapta a condus la Directii.StangaSauDreapta având o valoare de 3, după operația binară SAU. Putem vedea clar că valoarea 3 este atribuită și la Direcții.Sus, deci, nu, nici acest lucru nu ne ajută.
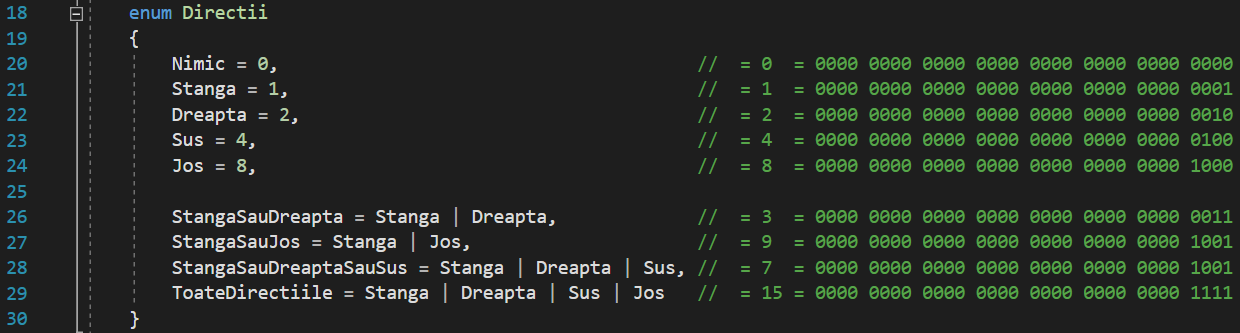
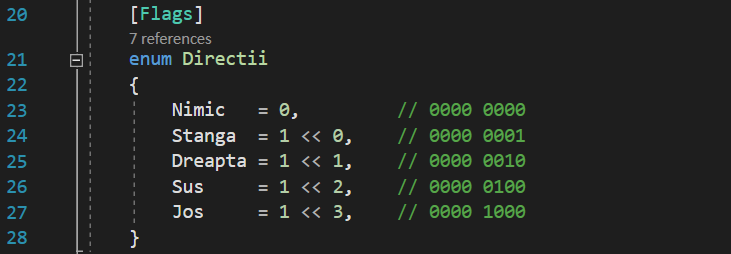
Soluția corectă la problema noastră ar fi de fapt stocarea tuturor elementelor enumerării noastre în așa fel încât fiecare dintre ele să aibă un singur bit cu o valoare de 1, pe o poziție diferită și unică față de restul celorlalte elemente. Ceva de genul:
Acum, fiecare dintre aceste patru valori binare este diferită, deoarece fiecare dintre ele are un singur bit cu o valoare de 1, fiecare din ei pe o poziție diferită. Dacă încercăm să folosim operația binară SAU pe oricare dintre ele acum, totul ar funcționa ireproșabil:
Putem concluziona din exemplele de mai sus că, din moment ce fiecare element al enumerării are un singur bit cu o valoare de 1, care se află într-un loc diferit pentru fiecare dintre elemente, nu am intra niciodată în conflict cu acești biți. Tocmai acest lucru îl ilustram mai devreme cu exemplul despre hârtia ce are câteva găuri și e folosită ca mască pentru vopseaua din spray. În cazul nostru, având doi operanzi cu câte 4 biți fiecare, putem spune că operația binară SAU acționează și ea ca o mască: pentru ca un bit cu o valoare de 1 să intre în rezultatul operației pe o anumită poziție, e necesiar ca cel puțin unul dintre biții operanzilor pe această poziție să fie 1, la fel ca o gaură în hârtie. Nu există găuri într-un anumit loc din hârtie, nu trece vopseaua. Nu exista nici un bit cu o valoare de 1 într-o anumită poziție în cel puțin unul dintre operanzi, nu trece nici o valoare binară 1 pentru acea poziție.
Din exercițiul mental de mai sus rezumăm faptul că trebuie să stocăm elementele enumerării noastre în așa fel încât reprezentarea lor binară să asigure un singur bit cu o valoare de 1 pentru fiecare valoare, și că bitul fiecărui element cu o valoare de 1 este pe o poziție unică în comparație cu toate celelalte elemente. Acest lucru este de fapt mai simplu de imaginat dacă ne uităm la câteva dintre aceste numere și la reprezentarea lor zecimală:
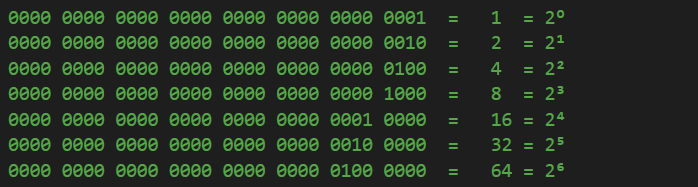
Cumva, avansând spre stânga poziția bitului cu o valoare de 1 cu un loc pentru fiecare dintre valori rezultă într-o valoare zecimală care este o putere consecutivă a lui 2. Ceea ce înseamnă că acestea sunt valorile pe care trebuie să le acordăm enumerării noastre:
Acum, avem tot o valoare de 1 pentru Directii.Stanga, 2 pentru Directii.Dreapta și 3 pentru Directii.StangaSauDreapta. Singura diferență, comparativ cu codul anterior, este că valoarea 3 nu este atribuită nici unui element al enumerării. Și putem testa pentru încă niște cazuri, chiar implicând combinații de mai mult de 2 operanzi, și vom obține în continuare același rezultat: nici una dintre valorile rezultate nu va fi egală cu valoarea vreunui element existent, prin urmare nu vom avea conflicte sau confuzii cu privire la ce elemente sunt utilizate:
Desigur, am putea folosi chiar reprezentarea hexazecimală a valorilor, astfel încât să nu jonglăm cu 32 de biți pentru fiecare număr, ci să le vedem în schimb ca perechi de 2 octeți pentru fiecare cifră hexazecimală, așa cum am explicat în lecția numere hexazecimale, astfel încât să folosim doar 8 cifre hexazecimale în loc de 32 de cifre binare:
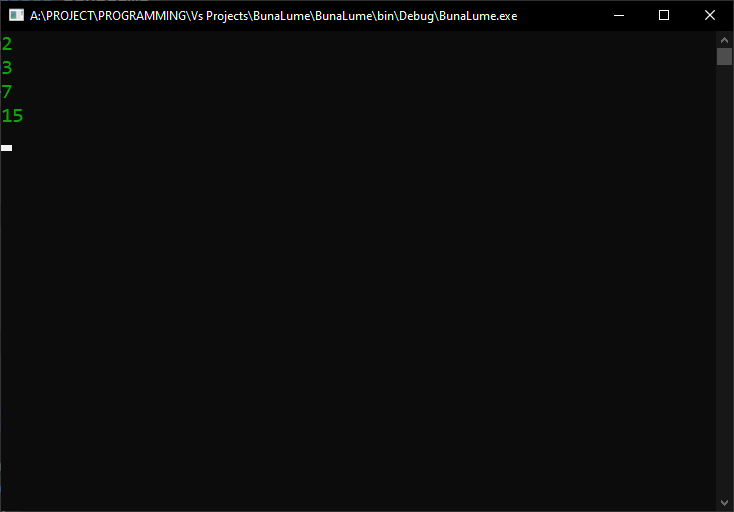
Mult mai ușor de văzut, gestionat și înțeles. Să încercăm să afișăm câteva dintre elementele combinate, pentru a vedea cum apar de fapt:
[raw][/raw]
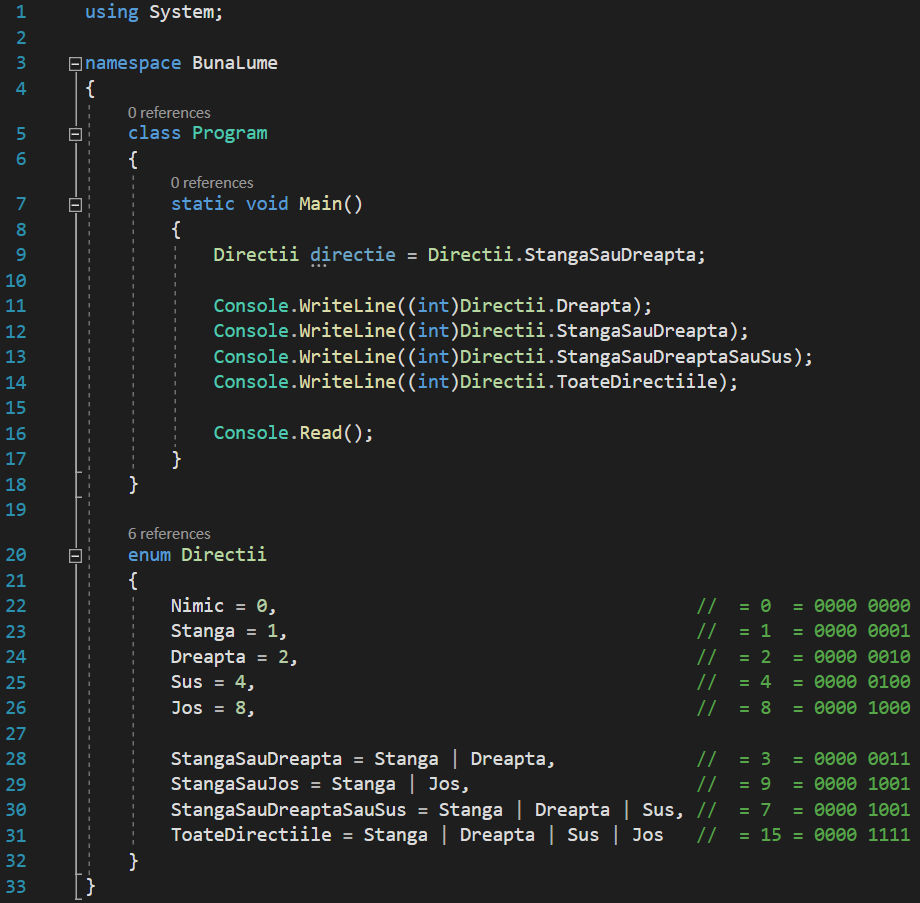
Cu acest rezultat:
Aceleași valori pe care le-am prezis. Cu toate acestea, ar fi foarte, foarte frumos să putem vedea numele elementelor enumerării care reprezintă aceste valori, decât să vedem valorile în sine. Trebuie să recunoașteți, Directii.StangaSauDreaptaSauSus este mult mai ușor de ținut minte ce înseamnă, în comparație cu 7. Să vedem cum arată, afișându-le direct pe consolă, fără a le converti valoarile într-un int în prealabil:
Iată și rezultatul:
Ceea ce este foarte frumos, vedem un nume semnificativ, în loc de o valoare numerică.
Cu toate acestea, ce se întâmplă dacă nu dorim să ne poluăm enumerarea cu valori combinate, cum ar fi Directii.StangaSauDreaptaSauSus sau Directii.StangaSauDreapta? Mai funcționează? Le mai putem combina oriunde avem nevoie de o combinație? Să încercăm:
[raw][/raw]
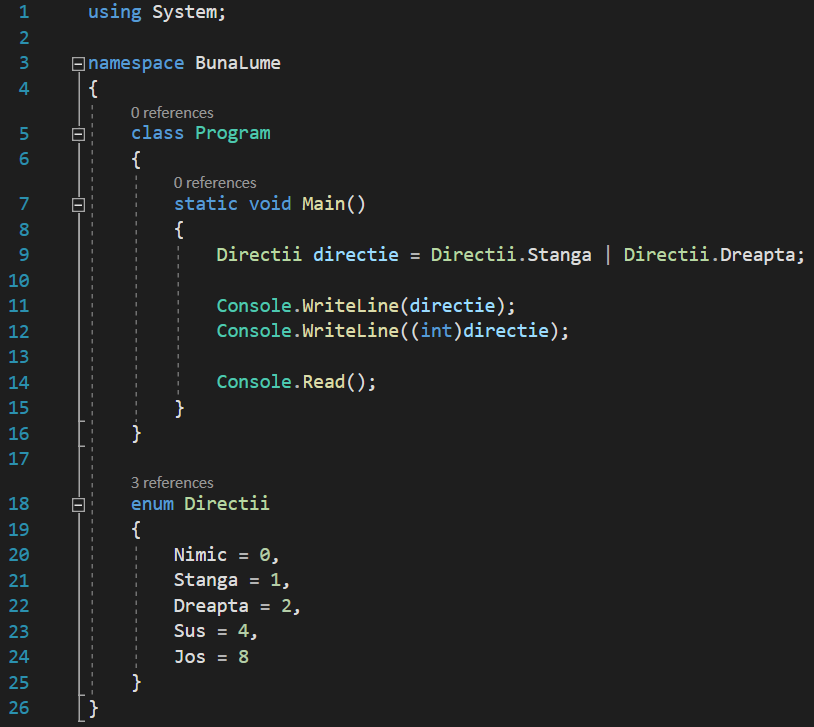
Și aici, rezultatul afișării valorii în mod direct și convertită într-un int:
Din păcate, de îndată ce am șters elementele combinate din enumerarea noastră, rezultatul afișării unei combinații a două elemente ale enumerării va fi în continuare doar o valoare numerică, chiar și fără a o converti într-un int. Deci, avem vreo soluție pentru a nu codifica aceste combinații în enumerările noastre și totuși să putem primi nume descriptive atunci când le tipărim la consolă?
Da, avem! Pentru a rezolva această problemă, enumerările pot fi decorate cu un atribut numit Flags, astfel:
Vizualizează schimbări cod
Legendă:
[/raw]

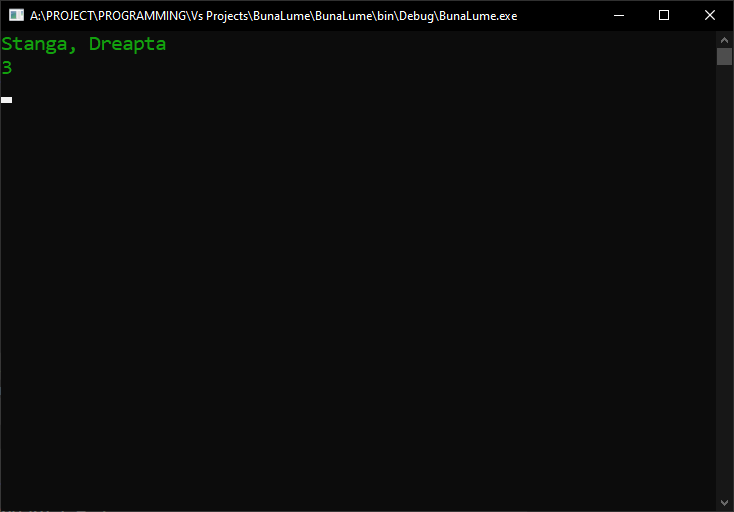
Acum, dacă rulăm programul din nou, vom vedea că deși enumerarea noastră nu mai conține elemente combinate în interiorul său, dacă și când alegem să combinăm astfel de elemente, acestea sunt afișate mult mai frumos la consolă:
Asta înseamnă că prin simpla plasare a atributului Flags deasupra enumerării, am instruit compilatorul să trateze de fapt elementele enumerării noastre ca măști de biți și să recunoască faptul că putem avea combinații de astfel de măști/elemente.
Deci, rețineți, atributul Flags NU ne acordă permisiunea de a folosi măști de biți, așa cum majoritatea programatorilor cred în mod incorect, de fapt spune doar compilatorului însuși că dorim ca elementele respectivei enumerări să fie tratate ca măști de biți, astfel încât să afișează combinațiile posibile ale acestora într-o formă mai frumoasă și mai inteligibilă. Dar, dacă nu ne pasă de modul în care sunt afișate, atâta timp cât elementelor enumerării li se atribuie valori folosind puteri ale lui 2, mascarea biților funcționează la fel de perfect, chiar și fără atributul Flags. Este recomandat să îl utilizați totusi, chiar dacă doar pentru a semnaliza altor programatori intenția utilizării enumerării.
Un alt lucru de reținut este faptul că doar specificarea atributului Flags pe o enumerare NU atribuie automat puterea ale lui 2 valorilor elementelor respectivei enumerări. Dacă nu specificați manual aceste valori, sau dacă nu le specificați în mod corect ca puteri unice ale lui 2, mascarea biților va eșua în continuare, chiar și atunci când utilizați atributul Flags.
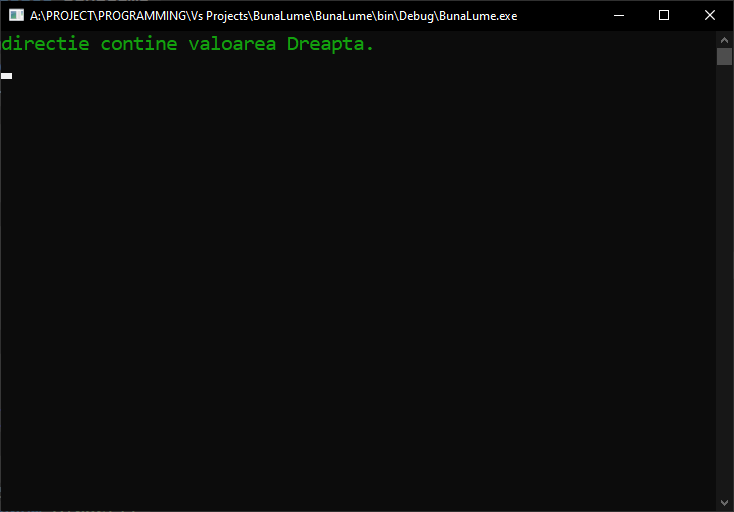
Dacă doriți să verificați dacă valoarea unui element de enumerare combinat conține un anumit element în interiorul acestuia, puteți utiliza funcția HasFlag() a enumerărilor, astfel:
[raw][/raw]
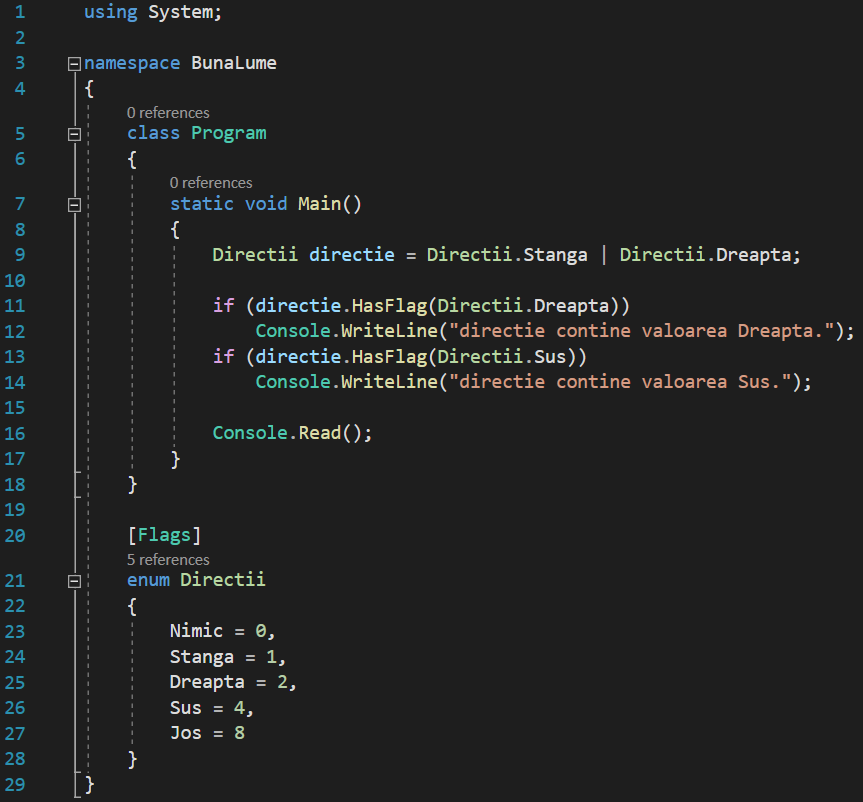
Iar consola va afișa asta:
Ceea ce este în concordanță cu intențiile noastre: variabila directie conține Directii.Dreapta, dar nu conține Directii.Sus.
Înainte de versiunea 4.0 a .NET framework, unde funcția HasFlag() nu există, am putea face aceeași verificare astfel:
[raw][/raw]
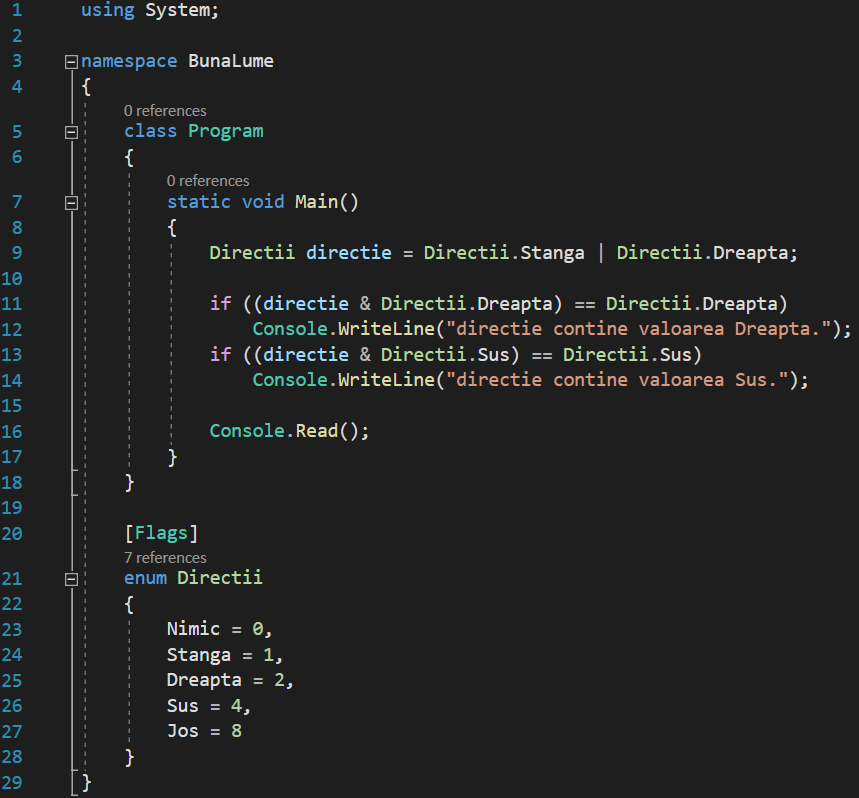
Iar rezultatul ar fi același. Explicația este simplă: executăm o operație ȘI pe biți și, așa cum știm deja, această operație returnează o valoare de 1 doar atunci când toți operanzii săi sunt 1 și 0 dacă la cel puțin unul dintre operanzi are valoarea 0.
Trebuie doar să ne uităm la reprezentarea hexazecimală a Directii.Stanga, Directii.Dreapta și Directii.StangaSauDreapta:
Acum, cu aceste valori, efectuăm o operațiune ȘI pe biți între valoarea variabilei directie (care este o combinație între Directii.Stanga și Directii.Dreapta) și valoarea Directii.Dreapta, și comparăm rezultatul cu reprezentarea hexazecimală a lui Direcții.Dreapta:
Comparația va fi True numai atunci când toată operațiunea ȘI pe biți va produce aceiași biți ca cei ai Directii.Dreapta. Și, da, putem vedea că o operațiune ȘI între variabila directie și Directii.Dreapta rezultă într-adevăr în aceeași biți ca cei ai Directii.Dreapta, iar compararea if returnează True.
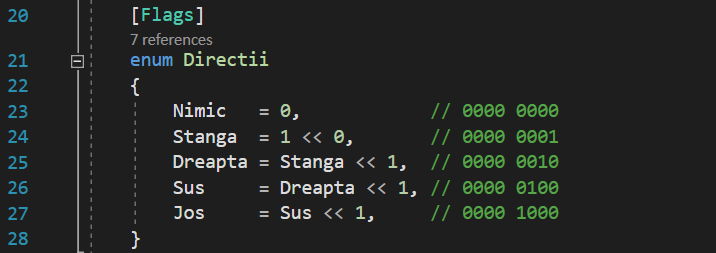
De asemenea, trebuie să știți că există un alt mod de a declara enumerări ca de măști de biți, utilizând operatorii de deplasare de biți. În loc să atribuim manual puterii consecutive și ascendente ale lui 2 valorilor elementelor, le putem atribui tuturor o valoare de 1, pe care o deplasăm apoi spre stânga cu un loc adițional pentru fiecare dintre valori:
Și enumerarea rezultată ar fi identică cu cea pe care am folosit-o anterior. Explicația este simplă: le atribuim tuturor elementelor valoarea 1, deoarece numărul întreg 1 este reprezentat binar ca un singur bit cu o valoare 1, pe ultima poziție a celor 32 de biți. De acolo, doar am deplasat acest bit cu un loc suplimentar pentru fiecare dintre valori, efectiv „mutându-l” pe următoarele locuri spre stânga.
Desigur, putem să deplasăm spre stânga fiecare valoare nouă folosind-o pe cea anterioară, schimbând biții cu un singur loc de fiecare dată, în loc de valori ascendente:
Aceeași tehnică de combinare a mai multor valori individuale într-o singură variabilă poate fi utilizată în locuri în care performanța este importantă. De exemplu, dacă doriți să creați o hartă de joc cu dimensiunea de 1.000 rânduri pe 1.000 coloane, aceasta înseamnă 1.000.000 celule. Dacă fiecare dintre aceste celule folosește câteva variabile pentru a păstra informații precum tipul de teren, dacă celula este ocupată sau nu de o clădire, dacă unitățile o pot traversa sau nu etc, vă puteți imagina că un milion de celule înmulțite cu câte variabile folosește fiecare celulă nu face bine memoriei RAM. În schimb, folosind măști de biți, este ușor să păstrați toate aceste informații într-o singură variabilă per celulă, în care fiecare bit al variabilei reprezintă o valoare diferită sau o combinație de valori.
Tags: binar, bit, deplasare de biți, flags, hexazecimal, mască de biți, operatori la nivel de bit